题目内容
用数学归纳法证明：“
+
+…+
≥1（ n∈N+）”时，在验证初始值不等式成立时，左边的式子应是“ ”．
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n+1 |
考点：数学归纳法
专题：计算题,点列、递归数列与数学归纳法
分析：分析不等式左边的项的特点，即可得出结论．
解答：
解：n=1时，左边的式子是
+
+
．
故答案为：
+
+
．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
故答案为：
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
点评：在利用数学归纳法证明问题中，第一步是论证n=1时结论是否成立，此时一定要分析不等式左边的项的特点，不能多写也不能少写，否则会引起答案的错误．
练习册系列答案
相关题目
如图所示是一个正方体的展开图，在原来的正方体中，有下列命题：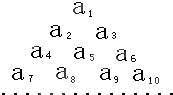
已知数列{an}是首项为1，公差为2的等差数列，将数列{an}中的各项排成如图所示的一个三角形数表，记A（i，j）表示第i行从左至右的第j个数，例如A（4，3）=a9，则A（10，4）=