题目内容
10.若三点A(0,2),B(2,5),C(3,b)能作为三角形的一个顶点,则实数b满足的条件是b≠$\frac{13}{2}$.分析 三点A(0,2),B(2,5),C(3,b)能作为三角形的一个顶点,可得三点A,B,C不共线,利用斜率计算公式即可得出.
解答 解:若三点A,B,C共线,则kAB=kAC,
∴$\frac{5-2}{2-0}$=$\frac{b-2}{3-0}$,解得b=$\frac{13}{2}$.
∵三点A(0,2),B(2,5),C(3,b)能作为三角形的一个顶点,
∴三点A,B,C不共线,
∴b≠$\frac{13}{2}$.
故答案为:b≠$\frac{13}{2}$.
点评 本题考查了三点共线问题、组成三角形的条件,考查了推理能力与技能数列,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
5.已知点C在直线AB上,P为平面上任意一点,且$\overrightarrow{PA}$=$\overrightarrow{PB}$+k$\overrightarrow{PC}$,则实数k的值为0.
15.已知向量$\overrightarrow{a}$=(1,1),|$\overrightarrow{OM}$|=1,$\overrightarrow{ON}$•$\overrightarrow{a}$=2,其中O为坐标原点,那么$\overrightarrow{MN}$•$\overrightarrow{a}$的最小值为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | 2 |
19.函数f(x)在x=1处可导,则当△x→0时,$\frac{f(1-2△x)-f(1)}{△x}$趋近于( )
| A. | -2f′(1) | B. | $\frac{1}{2}$f′(1) | C. | -$\frac{1}{2}$f′(1) | D. | f($\frac{1}{2}$) |

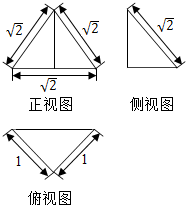 如图所示为一个几何体的三视图:
如图所示为一个几何体的三视图: ,则
,则 ( )
( ) B.
B. C.
C. D.
D.