题目内容
18.若三角形的一个顶点是A(2,1),两条角平分线所在的直线的方程为2x-y+3=0和x+y-2=0,求BC所在直线的方程.分析 由已知得AB与BC关于2x-y+3=0对称,AC与BC关于x+y-2=0对称,点A关于2x-y+3=0和x+y-2=0的对称点均在BC上,求出点A(2,1)关于直线2x-y+3=0和x+y-2=0的对称点为A′和A'',即可求出BC的直线方程.
解答 解:由题意,A不在两条角平分线上,
设A(2,1)关于2x-y+3=0的对称点为A′(a,b),
则$\left\{\begin{array}{l}{\frac{b-1}{a-2}=-\frac{1}{2}}\\{2×\frac{a+2}{2}-\frac{b+1}{2}+3=0}\end{array}\right.$,解得:a=-$\frac{14}{5}$,b=$\frac{17}{5}$
即A′(-$\frac{14}{5}$,b=$\frac{17}{5}$),
同理,A(2,1)关于x+y-2=0的对称点为A''(1,0),
∴BC的斜率为kBC=$\frac{17}{19}$,
∴BC的直线方程为y=$\frac{17}{19}$(x-1).
点评 本题考查直线方程的求法,是中档题,解题时要认真审题,注意直线的对称性质的合理运用.

练习册系列答案
相关题目
 如图所示,四边形OABC为等腰梯形,其中上底长为1,下底长为3,高为1,求梯形各边所在直线的斜率.
如图所示,四边形OABC为等腰梯形,其中上底长为1,下底长为3,高为1,求梯形各边所在直线的斜率.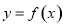 图象上不同两点
图象上不同两点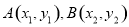 处的切线的斜率分别是
处的切线的斜率分别是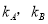 ,规定
,规定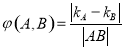 (
(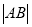 为线段AB的长度)叫做曲线
为线段AB的长度)叫做曲线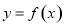 在点A与点B之间的“弯曲度”,给出以下命题:
在点A与点B之间的“弯曲度”,给出以下命题: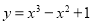 图象上两点A与B的横坐标分别为1和2,则
图象上两点A与B的横坐标分别为1和2,则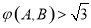 ;
;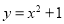 上不同的两点,则
上不同的两点,则 ;
;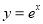 (e是自然对数的底数)上不同两点
(e是自然对数的底数)上不同两点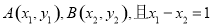 ,若
,若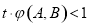 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是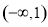 .
.