题目内容
2．已知i是虚数单位，若复数$\frac{z}{1+i}=2i$满足，则|z|=（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | $2\sqrt{2}$ | D． | 4 |
分析 把已知等式两边取模，化简整理得答案．
解答 解：由$\frac{z}{1+i}=2i$，得$|\frac{z}{1+i}|=|2i|$，
即|z|=$\sqrt{2}×2=2\sqrt{2}$．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．
练习册系列答案
相关题目
14．已知集合A={x∈Z||x-1|＜3}，B={x|x2+2x-3＜0}，则A∩B=（ ）
| A． | （-2，1） | B． | （1，4） | C． | {2，3} | D． | {-1，0} |
10．函数f（x）=$\sqrt{3}$sin2x+cos2x，则下列表述正确的是（ ）
| A． | f（x）在（-$\frac{π}{3}$，-$\frac{π}{6}$）单调递减 | B． | f（x）在（$\frac{π}{6}$，$\frac{π}{3}$）单调递增 | ||
| C． | f（x）在（-$\frac{π}{6}$，0）单调递减 | D． | f（x）在（0，$\frac{π}{6}$）单调递增 |
17．已知i是虚数单位，若复数$\frac{z}{1+i}=2i$满足，则复数z对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
11．已知函数f（x）=eax+b在（0，f（0））处的切线为y=x+1．
（1）若对任意x∈R，有f（x）≥kx成立，求实数k的取值范围．
（2）证明：对任意t∈（-∞，2]，f（x）＞t+lnx成立．
（1）若对任意x∈R，有f（x）≥kx成立，求实数k的取值范围．
（2）证明：对任意t∈（-∞，2]，f（x）＞t+lnx成立．
9．
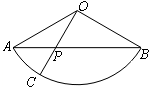如图，扇形AOB的圆心角为120°，点P在弦AB上，且$AP=\frac{1}{3}AB$，延长OP交弧AB于C．现向扇形AOB内投点，则该点落在扇形AOC内的概率为（ ）
如图，扇形AOB的圆心角为120°，点P在弦AB上，且$AP=\frac{1}{3}AB$，延长OP交弧AB于C．现向扇形AOB内投点，则该点落在扇形AOC内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{7}$ | D． | $\frac{3}{8}$ |