题目内容
9．
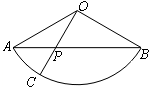如图，扇形AOB的圆心角为120°，点P在弦AB上，且$AP=\frac{1}{3}AB$，延长OP交弧AB于C．现向扇形AOB内投点，则该点落在扇形AOC内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{7}$ | D． | $\frac{3}{8}$ |
分析 求出扇形AOC的面积为$\frac{3π}{4}$，扇形AOB的面积为3π，从而得到所求概率．
解答 解：设OA=3，则$AB=3\sqrt{3}，AP=\sqrt{3}$，由余弦定理可求得$OP=\sqrt{3}$，有∠AOP=30°，
所以扇形AOC的面积为$\frac{3π}{4}$，扇形AOB的面积为3π，从而所求概率为$\frac{{\frac{3π}{4}}}{3π}=\frac{1}{4}$．
故选A．
点评 本题主要考查几何概型，正确求出扇形的面积是关键．
练习册系列答案
相关题目
2．已知i是虚数单位，若复数$\frac{z}{1+i}=2i$满足，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $2\sqrt{2}$ | D． | 4 |
3．为了对2016年某校中考成绩进行分析，在60分以上的全体同学中随机抽出8位，他们的数学分数（已折算为百分制）从小到大排是60、65、70、75、80、85、90、95，物理分数从小到大排是72、77、80、84、88、90、93、95．
（1）若规定85分以上为优秀，求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率；
（2）若这8位同学的数学、物理、化学分数事实上对应如下表：
①用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度；
②求y与x、z与x的线性回归方程（系数精确到0.01），当某同学的数学成绩为50分时，估计其物理、化学两科的得分．
参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）}（{{y_i}-\overline y}）}}{{\sqrt{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}•\sum_{i=1}^n{{{（{{y_i}-\overline y}）}^2}}}}$，
回归直线方程是：$\hat y=bx+a$，其中$b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}，a=\overline y-b\overline x$，
参考数据：$\overline x=77.5，\overline y=85，\overline z=81，\sum_{i=1}^8{{{（{{x_i}-\overline x}）}^2}≈1050，\sum_{i=1}^8{{{（{{y_i}-\overline y}）}^2}≈456}}$，$\sum_{i=1}^8{{{（{{z_i}-\overline z}）}^2}}≈550，\sum_{i=1}^8{（{{x_i}-\overline x}）（{{y_i}-\overline y}）≈688}$，$\sum_{i=1}^8{（{{x_i}-\overline x}）（{{z_i}-\overline z}）≈755}，\sqrt{1050}≈32.4$，$\sqrt{456}≈21.4，\sqrt{550}≈23.5$．
（1）若规定85分以上为优秀，求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率；
（2）若这8位同学的数学、物理、化学分数事实上对应如下表：
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
②求y与x、z与x的线性回归方程（系数精确到0.01），当某同学的数学成绩为50分时，估计其物理、化学两科的得分．
参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）}（{{y_i}-\overline y}）}}{{\sqrt{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}•\sum_{i=1}^n{{{（{{y_i}-\overline y}）}^2}}}}$，
回归直线方程是：$\hat y=bx+a$，其中$b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}，a=\overline y-b\overline x$，
参考数据：$\overline x=77.5，\overline y=85，\overline z=81，\sum_{i=1}^8{{{（{{x_i}-\overline x}）}^2}≈1050，\sum_{i=1}^8{{{（{{y_i}-\overline y}）}^2}≈456}}$，$\sum_{i=1}^8{{{（{{z_i}-\overline z}）}^2}}≈550，\sum_{i=1}^8{（{{x_i}-\overline x}）（{{y_i}-\overline y}）≈688}$，$\sum_{i=1}^8{（{{x_i}-\overline x}）（{{z_i}-\overline z}）≈755}，\sqrt{1050}≈32.4$，$\sqrt{456}≈21.4，\sqrt{550}≈23.5$．
17．已知在△ABC中，∠ACB=90°，BC=3，AC=4，P是线段AB上的点，则P到AC，BC的距离的乘积的最大值为（ ）
| A． | 3 | B． | 2 | C． | $2\sqrt{3}$ | D． | 9 |
4．圆（x-2）2+y2=4关于直线$y=\frac{{\sqrt{3}}}{3}x$对称的圆的方程是（ ）
| A． | ${（x-\sqrt{3}）^2}+{（y-1）^2}=4$ | B． | ${（x-\sqrt{2}）^2}+{（y-\sqrt{2}）^2}=4$ | C． | x2+（y-2）2=4 | D． | ${（x-1）^2}+{（y-\sqrt{3}）^2}=4$ |
1．已知定义域为R的函数f（x）的图象经过点（1，1），且对任意实数x1＜x2，都有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}＞-2$，则不等式$f（{log_2}|{3^x}-1|）＜3-{log_{\sqrt{2}}}|{3^x}-1|$的解集为（ ）
| A． | （-∞，0）∪（0，1） | B． | （0，+∞） | C． | （-1，0）∪（0，3） | D． | （-∞，1） |
满足约束条件
，则目标函数
的取值范围为___________．