题目内容
11.已知函数f(x)=eax+b在(0,f(0))处的切线为y=x+1.(1)若对任意x∈R,有f(x)≥kx成立,求实数k的取值范围.
(2)证明:对任意t∈(-∞,2],f(x)>t+lnx成立.
分析 (1)通过讨论k的范围,结合函数的单调性求出k的具体范围即可;
(2)法一:构造函数h(x)=ex-lnx-t(x>0)(t≤2),根据函数的单调性证明即可;
法二:问题转化为证ex>2+lnx,令h(x)=ex-lnx-2,h′(x)=ex-$\frac{1}{x}$=$\frac{x{e}^{x}-1}{x}$(x>0),根据函数的单调性证明即可.
解答 解:(1)由f′(x)=eax得k=f′(0)=a=1,
由切点(0,f(0))在切线y=x+1上,得f(0)=1,
所以切点为(0,1),由点(0,1)在f(x)=eax+b上,
得b=0,所以f(x)=ex…(2分)
当k<0时,对于x∈R,ex≥kx显然不恒成立
当k=0时,ex≥kx显然成立…(3分)
当k>0时,若要ex-kx≥0恒成立,必有(ex-kx)min≥0
设t(x)=ex-kx,则t′(x)=ex-k
易知t(x)在(-∞,lnk)上单调递减,在(lnk,+∞)上单调递增,则t(x)min=k(1-lnk)
若ex-kx≥0恒成立,即t(x)min=k(1-lnk)≥0,得0<k≤e
综上得0≤k≤e…(6分)
(2)证法1:由(1)知ex≥ex成立,构造函数h(x)=ex-lnx-t(x>0)(t≤2)
h′(x)=e-$\frac{1}{x}$=$\frac{ex-1}{x}$所以$h{(x)_{min}}=h(\frac{1}{e})=1-ln\frac{1}{e}-t=2-t≥0$(t≤2)
有ex≥lnx+t成立(当$x=\frac{1}{e},t=2$时取等号).由(1)知ex≥ex成立(当x=1时取等号),
所以有ex>t+lnx成立,即对任意t∈(-∞,2],f(x)>t+lnx成立…(12分)
证法2,因为t≤2,所以要证ex>t+lnx,只须证ex>2+lnx
令h(x)=ex-lnx-2,h′(x)=ex-$\frac{1}{x}$=$\frac{x{e}^{x}-1}{x}$(x>0),
令t(x)=xex-1,t′(x)=ex+xex>0,所以t(x)在(0,+∞)递增,
t(x)>t(0)=-1,由于t(0)=-1<0,t(1)=e-1>0
所以存在x0∈(0,1),有$t({x_0})={x_0}{e^{x_0}}-1=0$,则${e^{x_0}}=\frac{1}{x_0}$,x0=-lnx0
即h′(x)>0得x>x0,h′(x)<0得0<x<x0
所以$h(x)≥h({x_0})={e^{x_0}}-ln{x_0}-2=\frac{1}{x_0}+{x_0}-2>2-2=0$
所以ex-2-lnx>0成立,即ex>t+lnx成立
即对任意t∈(-∞,2],f(x)>t+lnx成立…(12分)
点评 本题考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.

| A. | $\sqrt{5}$ | B. | 5 | C. | $\frac{\sqrt{85}}{2}$ | D. | $\frac{85}{4}$ |
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
| A. | 2$\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | 8$\sqrt{2}$-8 | D. | 2$\sqrt{2}$-2 |
(1)若规定85分以上为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2)若这8位同学的数学、物理、化学分数事实上对应如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
②求y与x、z与x的线性回归方程(系数精确到0.01),当某同学的数学成绩为50分时,估计其物理、化学两科的得分.
参考公式:相关系数$r=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})}({{y_i}-\overline y})}}{{\sqrt{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}•\sum_{i=1}^n{{{({{y_i}-\overline y})}^2}}}}$,
回归直线方程是:$\hat y=bx+a$,其中$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}},a=\overline y-b\overline x$,
参考数据:$\overline x=77.5,\overline y=85,\overline z=81,\sum_{i=1}^8{{{({{x_i}-\overline x})}^2}≈1050,\sum_{i=1}^8{{{({{y_i}-\overline y})}^2}≈456}}$,$\sum_{i=1}^8{{{({{z_i}-\overline z})}^2}}≈550,\sum_{i=1}^8{({{x_i}-\overline x})({{y_i}-\overline y})≈688}$,$\sum_{i=1}^8{({{x_i}-\overline x})({{z_i}-\overline z})≈755},\sqrt{1050}≈32.4$,$\sqrt{456}≈21.4,\sqrt{550}≈23.5$.
| A. | 3 | B. | 2 | C. | $2\sqrt{3}$ | D. | 9 |
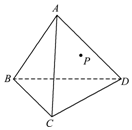 如图,有一个正三棱锥的零件,P是侧面ACD上的一点.过点P作一个与棱AB垂直的截面,怎样画法?并说明理由.
如图,有一个正三棱锥的零件,P是侧面ACD上的一点.过点P作一个与棱AB垂直的截面,怎样画法?并说明理由.