题目内容
已知函数y=f(x)=
sin(
+2x)+1.
(1)求函数f(x)的最大值和最小值以及取最大、最小值时相应x的取值集合;
(2)写出函数f(x)的单调递增区间.
(3)作出此函数在一个周期内的图象.
| 2 |
| π |
| 4 |
(1)求函数f(x)的最大值和最小值以及取最大、最小值时相应x的取值集合;
(2)写出函数f(x)的单调递增区间.
(3)作出此函数在一个周期内的图象.
考点:正弦函数的单调性,三角函数的最值
专题:三角函数的求值,三角函数的图像与性质
分析:(1)对于函数函数y=
sin(2x+
)+1,利用正弦函数的图象和性质求得其最大值和最小值,并写出取得最值是相应的x的集合.
(2)令2kπ-
≤2x+
≤2kπ+
,k∈z,求得x的范围,可得函数的增区间.
(3)根据五点法作图的方法先取值,然后描点即可得到图象.
| 2 |
| π |
| 4 |
(2)令2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
(3)根据五点法作图的方法先取值,然后描点即可得到图象.
解答:
解:(1)对于函数函数y=1+
sin(2x+
),当2x+
=2kπ+
,k∈z时,函数取得最大值为
+1,此时,x=kπ+
,k∈z.
当2x+
=2kπ-
,k∈z时,函数取得最小值为1-
,此时,x=kπ-
,k∈z.
(2)令2kπ-
≤2x+
≤2kπ+
,k∈z,求得 kπ-
≤x≤kπ+
,k∈z.
故函数的增区间为[kπ-
,kπ+
],k∈z.
(3)解:列表:…(6分)
描点、连线如图所示.…(12分)
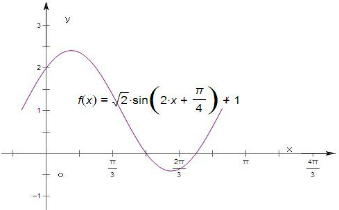
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| 2 |
| π |
| 8 |
当2x+
| π |
| 4 |
| π |
| 2 |
| 2 |
| 3π |
| 8 |
(2)令2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
故函数的增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
(3)解:列表:…(6分)
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
| y | 1 | 1+
| 1 | 1-
| 1 |
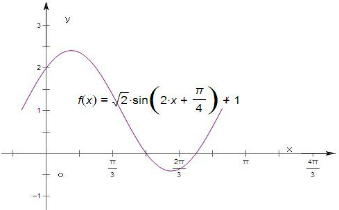
点评:本题主要考查正弦函数的图象和性质,五点作图法,属于基本知识的考查.

练习册系列答案
相关题目
下列命题错误的是( )
| A、命题“若x2<1,则-1<x<1”的逆否命题是若x≥1或x≤-1,则x2≥1 |
| B、“am2<bm2”是”a<b”的充分不必要条件 |
| C、命题p:存在x0∈R,使得x02+x0+1<0,则¬p:任意x∈R,都有x2+x+1≥0 |
| D、命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 |

