题目内容
设m∈R,过定点A的动直线l1:x+my=0和过定点B的动直线l2:mx-y-m+3=0=0交于点P(x,y),
(I) 试判断直线l1与l2的位置关系;
(Ⅱ) 求|PA|•|PB|的最大值.
(I) 试判断直线l1与l2的位置关系;
(Ⅱ) 求|PA|•|PB|的最大值.
考点:两点间的距离公式,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:(I)对m分类讨论,利用两条直线相互垂直与斜率的关系即可得出;
(II)当m=0时,直接求出;当m≠0时,点P在以AB为直径的圆上,可得|PA|2+|PB|2=|AB|2=10,利用基本不等式的性质即可得出.
(II)当m=0时,直接求出;当m≠0时,点P在以AB为直径的圆上,可得|PA|2+|PB|2=|AB|2=10,利用基本不等式的性质即可得出.
解答:
解:( I)当m=0时,两条直线方程分别化为:x=0,-y+3=0,此时两条直线垂直;
当m≠0时,两条直线的斜率分别为:-
,m,则-
×m=-1,因此两条直线垂直.
故直线l1与l2垂直;
( II)由直线l1:x+my=0可得定点A(0,0);
由直线l2:mx-y-m+3=0=0化为m(x-1)+(3-y)=0,联立
,解得x=1,y=3.
可得定点B(1,3).
当m=0时,两条直线的交点为(0,3),则|PA|•|PB|=
×
=3.
当m≠0时,点P在以AB为直径的圆上,
∴|PA|2+|PB|2=|AB|2=10,
∴10≥2|PA|•|PB|,
∴|PA|•|PB|≤5.
综上可得:|PA|•|PB|的最大值为5.
当m≠0时,两条直线的斜率分别为:-
| 1 |
| m |
| 1 |
| m |
故直线l1与l2垂直;
( II)由直线l1:x+my=0可得定点A(0,0);
由直线l2:mx-y-m+3=0=0化为m(x-1)+(3-y)=0,联立
|
可得定点B(1,3).
当m=0时,两条直线的交点为(0,3),则|PA|•|PB|=
| 0+32 |
| 12+0 |
当m≠0时,点P在以AB为直径的圆上,
∴|PA|2+|PB|2=|AB|2=10,
∴10≥2|PA|•|PB|,
∴|PA|•|PB|≤5.
综上可得:|PA|•|PB|的最大值为5.
点评:本题考查了两条直线相互垂直与斜率的关系、圆的性质、基本不等式的性质、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
tan
=( )
| 5π |
| 6 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
设实数x,y满足不等式组
,则
的取值范围是( )
|
| y |
| x+3 |
A、[0,
| ||||
B、[
| ||||
C、[0,
| ||||
D、[
|
下列说法中正确的是( )
| A、一个命题的逆命题为真,则它的逆否命题一定为真 |
| B、一个命题的否命题为真,则它的逆命题一定为真 |
| C、“a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
| D、“a>b”与“a+c>b+c”不等价 |
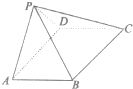 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.