题目内容
设定义在R上的函数f（x）=x|x|，则f（x）（ ）
| A、只有最大值 |
| B、只有最小值 |
| C、既有最大值，又有最小值 |
| D、既无最大值，又无最小值 |
考点：函数的值域
专题：函数的性质及应用
分析：先绝对值，再求出函数的值域，问题得以解决．
解答：
解：当x≥0时，f（x）=x2≥0，故f（x）的值域为[0，+∞），
当x＜0时，f（x）=-x2＜0，故f（x）的值域为（-∞，0），
因此定义在R上的函数f（x）=x|x|的值域为（-∞，+∞），
故选：D．
当x＜0时，f（x）=-x2＜0，故f（x）的值域为（-∞，0），
因此定义在R上的函数f（x）=x|x|的值域为（-∞，+∞），
故选：D．
点评：本题主要考查了含有绝对值函数的值域的求法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
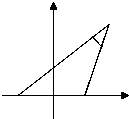设动点P到点A（-1，0）和B（1，0）的距离分别为d1和d2，∠APB=2θ，且存在常数λ（0＜λ＜1），使得d1d2sin2θ=λ（如图所示），那么点P的轨迹是（ ）| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
如图是一个几何体的三视图，其中“正视图”是一个边长为2的正方形，“俯视图”是一个正三角形，则这个三视图中“侧视图”的面积为（ ）sin300°+tan240°的值是（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
y=sin（
x-
），x∈（
，2π）的最大值是（ ）
| 1 |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
A、
| ||||
| B、1 | ||||
C、-
| ||||
D、
|
下列函数既是偶函数，又在区间（-∞，0）上为增函数的是（ ）
| A、y=-2x | ||
| B、y=-x2 | ||
| C、y=|x| | ||
D、y=-
|
若一个棱锥的各棱长均相等，则该棱锥一定不是（ ）
| A、三棱锥 | B、四棱锥 |
| C、五棱锥 | D、六棱锥 |
设函数y=
的定义域为M，那么（ ）
| x | ||
|
| A、{x|x＞-1且x≠0} |
| B、{x|x＞-1} |
| C、M={x|x＜-1或x＞0} |
| D、M={x|x＜-1或-1＜x＜0或x＞0} |