题目内容
2.若f(x)=|log2x|-m有两个零点x1,x2(x1>x2),则${x_1}^2+4{x_2}^2$的最小值为4.分析 由题意可知:求得f(x)的两个零点,则${x_1}^2+4{x_2}^2$=22m+4($\frac{1}{2}$)2m=22m+22-2m≥2$\sqrt{{2}^{2m}•{2}^{2-2m}}$=2$\sqrt{{2}^{2m+2-2m}}$=4.
解答 解:由题意可知:f(x)=|log2x|-m有两个零点x1,x2(x1>x2),则x1=2m,x2=($\frac{1}{2}$)m,
${x_1}^2+4{x_2}^2$=22m+4($\frac{1}{2}$)2m=22m+22×2-2m=22m+22-2m≥2$\sqrt{{2}^{2m}•{2}^{2-2m}}$=2$\sqrt{{2}^{2m+2-2m}}$=4,
∴${x_1}^2+4{x_2}^2$的最小值4.
故答案为:4.
点评 本题考查函数零点定理的判定,考查含绝对值的函数的零点判断,基本不等式的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.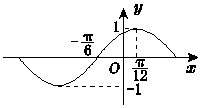 已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )
 已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=sin({x+\frac{π}{3}})$ | C. | $y=sin({2x-\frac{2π}{3}})$ | D. | $y=sin({2x+\frac{π}{3}})$ |