题目内容
3．已知实数x，y满足2x+y+10=0，那么$\sqrt{{x^2}+{y^2}}$的最小值为（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{10}$ | C． | $2\sqrt{5}$ | D． | $2\sqrt{10}$ |
分析 利用点到直线的距离公式即可得出．
解答 解：$\sqrt{{x^2}+{y^2}}$的最小值为原点到直线的距离d=$\frac{10}{\sqrt{{2}^{2}+{1}^{2}}}$=2$\sqrt{5}$．
故选：C．
点评 本题考查了点到直线的距离公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
11．
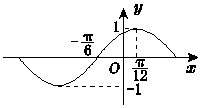已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）
已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）| A． | $y=sin（{x+\frac{π}{6}}）$ | B． | $y=sin（{x+\frac{π}{3}}）$ | C． | $y=sin（{2x-\frac{2π}{3}}）$ | D． | $y=sin（{2x+\frac{π}{3}}）$ |
18．已知圆的一般方程为x2+y2+Dx+Ey+F=0，则圆心坐标是（ ）
| A． | $（{\frac{E}{2}，\frac{D}{2}}）$ | B． | $（{-\frac{E}{2}，-\frac{D}{2}}）$ | C． | $（{\frac{D}{2}，\frac{E}{2}}）$ | D． | $（{-\frac{D}{2}，-\frac{E}{2}}）$ |
15．i是虚数单位，i2012等于（ ）
| A． | 1 | B． | -1 | C． | i | D． | -i |