题目内容
16．直线x+y-2=0和x-y-4=0的交点为（ ）| A． | （3，-1） | B． | （-3，-1） | C． | （-3，1） | D． | （3，1） |
分析 把直线方程联立即可得出．
解答 解：联立$\left\{\begin{array}{l}{x+y-2=0}\\{x-y-4=0}\end{array}\right.$，解得x=3，y=-1．
∴交点为（3，-1）．
故选：A．
点评 本题考查了直线相交交点问题，考查了分类讨论方法、推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
11．
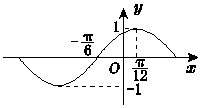已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）
已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）| A． | $y=sin（{x+\frac{π}{6}}）$ | B． | $y=sin（{x+\frac{π}{3}}）$ | C． | $y=sin（{2x-\frac{2π}{3}}）$ | D． | $y=sin（{2x+\frac{π}{3}}）$ |
1．点P（2，4）关于直线x+y+1=0的对称点的坐标为（ ）
| A． | （5，-3） | B． | （3，-5） | C． | （-5，3） | D． | （-5，-3） |
6．从一批苹果中随机抽取100个作为样本，其重量（单位：克）的频数分布表如下：
（1）在频率分布直方图中，求分组重量在[85，95）对应小矩形的高；
（2）利用频率估计这批苹果重量的平均数．
（3）用分层抽样的方法从重量在[85，95）和[105，115）的苹果中抽取5个，从这5个苹果任取2个，求重量在这两个组中各有1个的概率．
| 分组（重量） | [75，85） | [85，95） | [95，105） | [105，115） |
| 频数（个） | 15 | 30 | 35 | 20 |
（2）利用频率估计这批苹果重量的平均数．
（3）用分层抽样的方法从重量在[85，95）和[105，115）的苹果中抽取5个，从这5个苹果任取2个，求重量在这两个组中各有1个的概率．