题目内容
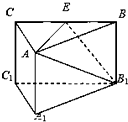 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中:
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中:①CC1与B1E是异面直线;
②AC⊥底面A1B1BA;
③二面角A-B1E-B为钝角;
④A1C∥平面AB1E.
其中正确命题的序号为
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①CC1与B1E在同一个平面,不是异面直线;
②AE⊥底面A1B1BA,即可判断出;
③由AE⊥底面A1B1BA,因此二面角A-B1E-B为直角;
④如图所示,连接A1B交AB1于点O,连接EO,利用三角形的中位线定理可得:EO∥A1C,利用线面平行的判定定理即可得出:A1C∥平面AB1E.
②AE⊥底面A1B1BA,即可判断出;
③由AE⊥底面A1B1BA,因此二面角A-B1E-B为直角;
④如图所示,连接A1B交AB1于点O,连接EO,利用三角形的中位线定理可得:EO∥A1C,利用线面平行的判定定理即可得出:A1C∥平面AB1E.
解答:
解:①CC1与B1E在同一个平面,不是异面直线,不正确;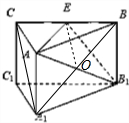
②AE⊥底面A1B1BA,因此不正确;
③由AE⊥底面A1B1BA,因此二面角A-B1E-B为直角,因此不正确;
④如图所示,连接A1B交AB1于点O,连接EO,则EO∥A1C,∵EO?平面AB1E,A1C?平面AB1E.∴A1C∥平面AB1E.
综上可得:其中正确命题的序号为 ④.
故答案为:④.

②AE⊥底面A1B1BA,因此不正确;
③由AE⊥底面A1B1BA,因此二面角A-B1E-B为直角,因此不正确;
④如图所示,连接A1B交AB1于点O,连接EO,则EO∥A1C,∵EO?平面AB1E,A1C?平面AB1E.∴A1C∥平面AB1E.
综上可得:其中正确命题的序号为 ④.
故答案为:④.
点评:本题考查了空间中线线、线面平行与垂直的位置关系判定,考查了推理能力,考查了空间想象能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=sinxcosx+
cos2x-
.
(1)求函数f(x)的最小正周期及单调递减区间;
(2)如果△ABC的角A,B,C所对的边为a,b,c,且满足b2=ac,试求f(B)的取值范围.
| 3 |
| ||
| 2 |
(1)求函数f(x)的最小正周期及单调递减区间;
(2)如果△ABC的角A,B,C所对的边为a,b,c,且满足b2=ac,试求f(B)的取值范围.
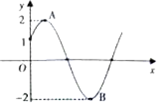 若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤
若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤| π |
| 2 |
A、ω=
| ||||
B、ω=
| ||||
C、ω=
| ||||
D、ω=
|
设(2x+
)n(n∈N+)的展开式的各项系数的和为A,展开式的二项式系数的和为B,若
=
,则展开式中x3的系数为( )
| 1 | ||
|
| A |
| B |
| 729 |
| 64 |
| A、160 | B、240 |
| C、320 | D、480 |
已知x,y满足约束条件
,则z=(x+3)2+y2的最小值为( )
|
| A、8 | B、10 | C、12 | D、16 |
设f(x)=15x5-24x4+33x3-42x2+51x,用秦九韶算法求f(2)的值为( )
| A、147 | B、294 |
| C、699 | D、1398 |