题目内容
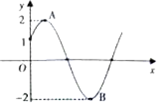 若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤
若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤| π |
| 2 |
A、ω=
| ||||
B、ω=
| ||||
C、ω=
| ||||
D、ω=
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:计算题,三角函数的图像与性质
分析:由函数图象经过点(0,1),代入解析式得sinφ=
,解出φ=
.根据A、B两点之间的距离为5,由勾股定理解出横坐标的差为3,得函数的周期T=6,由此算出ω=
.
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
解答:
解:∵函数图象经过点(0,1),
∴f(0)=2sinφ=1,可得sinφ=
,
又∵0≤φ≤
,
∴φ=
.
∵其中A、B两点的纵坐标分别为2、-2,
∴设A、B的横坐标之差为d,则|AB|=
=5,解之得d=3,
由此可得函数的周期T=6,得
=6,解之得ω=
.
故选:C.
∴f(0)=2sinφ=1,可得sinφ=
| 1 |
| 2 |
又∵0≤φ≤
| π |
| 2 |
∴φ=
| π |
| 6 |
∵其中A、B两点的纵坐标分别为2、-2,
∴设A、B的横坐标之差为d,则|AB|=
| d2+(-2-2)2 |
由此可得函数的周期T=6,得
| 2π |
| ω |
| π |
| 3 |
故选:C.
点评:本题给出正弦型三角函数的图象,确定其解析式并求f(-1)的值.着重考查了勾股定理、由y=Asin(ωx+φ)的部分图象确定其解析式等知识,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
已知O为坐标原点,A(-1,1),B为圆x2+y2=9上的一个动点,则线段AB的中垂线与线段OB的交点E的轨迹是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
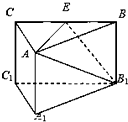 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中:
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中: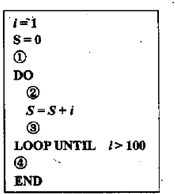 如图的语句是求S=1+2+3+…+100的一个程序,语句i=i+1应当在这个程序中的①②③④四处的哪一处才能实现上述功能( )
如图的语句是求S=1+2+3+…+100的一个程序,语句i=i+1应当在这个程序中的①②③④四处的哪一处才能实现上述功能( )