题目内容

设f（x）=15x5-24x4+33x3-42x2+51x，用秦九韶算法求f（2）的值为（　　）
A、147B、294
C、699D、1398
考点：秦九韶算法
专题：算法和程序框图
分析：由于f（x）=15x5-24x4+33x3-42x2+51x=（（（（15x-24）x+33）x-42）x+51）x，利用秦九韶算法即可得出．
解答： 解：∵f（x）=15x5-24x4+33x3-42x2+51x=（（（（15x-24）x+33）x-42）x+51）x，
∴v0=15，v1=15×2-24=6，v2=6×2+33=45，v3=45×2-42=48，v4=48×2+51=147，v5=147×2=294．
故选：B．
点评：本题考查了秦九韶算法，属于基础题．
练习册系列答案
相关题目
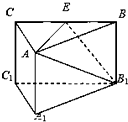如图，三棱柱A1B1C1-ABC中，侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC中点，则下列命题中：
①CC1与B1E是异面直线；
②AC⊥底面A1B1BA；
③二面角A-B1E-B为钝角；
④A1C∥平面AB1E．
其中正确命题的序号为
 
．（写出所有正确命题的序号）
已知集合A={x|a2x2+4x+4=0}．
（1）若A中至少有一个元素，求a的取值范围；
（2）若A中至多只有一个元素，求a的取值范围．
求函数y=log0.5（4-x2）的单调区间．
解方程：x3-3x+2=0．
已知实数x，y满足
x+2≥0
x-y≤0
0≤y≤k
，z=x+y，若z的最大值为12，则z的最小值为
 
．
已知点A（x，y）是30°角终边上异于原点的一点，则
y
x
等于（　　）
A、
3
B、-
3
C、
3
3
D、-
3
3
数列{an}中，a1=1，a2=λ+1，an+1=
an+2+λan
1+λ
（λ≠-1），n∈N*
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设Sn为数列{an}的前n项和，当λ＞0且λ≠1时，比较Sn+
n
λ-1
与3an的大小．
设函数f（x）是定义在（-2，0）上的可导函数，其导函数为f′（x），且有2f（x）+xf′（x）＞x2，则不等式（x+2014）2f（x+2014）-f（-1）＞0的解集为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网