题目内容
已知x,y满足约束条件
,则z=(x+3)2+y2的最小值为( )
|
| A、8 | B、10 | C、12 | D、16 |
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,数形结合得到最优解,由z=(x+3)2+y2的几何意义得答案.
解答:
解:由约束条件
作出可行域如图,

z=(x+3)2+y2的几何意义为可行域内的动点(x,y)到定点M(-3,0)的距离的平方.
由点M(-3,0)到直线x+y-1=0的距离d=
=2
.
∴z=(x+3)2+y2的最小值为8.
故选:A.
|

z=(x+3)2+y2的几何意义为可行域内的动点(x,y)到定点M(-3,0)的距离的平方.
由点M(-3,0)到直线x+y-1=0的距离d=
| |-3-1| | ||
|
| 2 |
∴z=(x+3)2+y2的最小值为8.
故选:A.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在一次篮球投篮比赛中,甲、乙两名球员各投篮一次,设命题p:“甲球员投篮命中”,q:“乙球员投篮命中”,则命题“至少有一名球员没有投中”可表示为( )
| A、p∨q |
| B、p∨(¬q) |
| C、(¬p)∧(¬q) |
| D、(¬p)∨(¬q) |
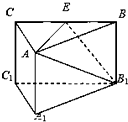 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中:
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中: