题目内容
(1)求证:
=
(2)证明
=
-
.
| tanα•sinα |
| tanα-sinα |
| tanα+sinα |
| tanαsinα |
(2)证明
| 2(cosα-sinα) |
| 1+sinα+cosα |
| cosα |
| 1+sinα |
| sinα |
| 1+cosα |
考点:三角函数恒等式的证明
专题:三角函数的求值
分析:(1)利用商的关系、二倍角公式分别化简左边和右边,即可证明原结论成立;
(2)利用平方关系、商的关系,二倍角公式分别化简左边和右边,即可证明原结论成立.
(2)利用平方关系、商的关系,二倍角公式分别化简左边和右边,即可证明原结论成立.
解答:
证明:(1)左边=
=
=
=
,
右边=
=
=
=
,
所以左边=右边,即原结论成立;
(2)左边=
=
,
右边=
-
=
-
=
=
所以左边=右边,即原结论成立.
| ||
|
| sinα |
| 1-cosα |
2sin
| ||||
2sin2
|
cos
| ||
sin
|
右边=
| ||
|
| 1+cosα |
| sinα |
2cos2
| ||||
2sin
|
cos
| ||
sin
|
所以左边=右边,即原结论成立;
(2)左边=
| 2(cosα-sinα) | ||||||
2cos2
|
| cosα-sinα | ||||||
cos
|
右边=
cos2
| ||||||||
sin2
|
2sin
| ||||
2cos2
|
=
cos
| ||||
sin
|
sin
| ||
cos
|
cos2
| ||||||||||||
cos
|
=
| cosα-sinα | ||||||
cos
|
所以左边=右边,即原结论成立.
点评:本题考查平方关系、商的关系,二倍角公式,熟练掌握公式是解题的关键,考查化简、变形能力.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
在△ABC中,角A,B,C的对边分别为a,b,c,若cos2
=
,则△ABC的形状为( )
| B |
| 2 |
| a+c |
| 2c |
| A、直角三角形 |
| B、锐角三角形 |
| C、等腰三角形 |
| D、钝角三角形 |
在一次篮球投篮比赛中,甲、乙两名球员各投篮一次,设命题p:“甲球员投篮命中”,q:“乙球员投篮命中”,则命题“至少有一名球员没有投中”可表示为( )
| A、p∨q |
| B、p∨(¬q) |
| C、(¬p)∧(¬q) |
| D、(¬p)∨(¬q) |
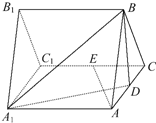 如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.
如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.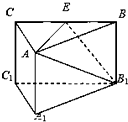 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中:
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列命题中: