Question

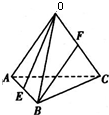
已知空间四边形OABC各边及对角线长都相等，E，F分别为AB，OC的中点，则异面直线OE与BF所成角的余弦值为（　　）

• A、

  1

  3

• B、-

  1

  3

• C、

  2

  3

• D、-

  2

  3

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：设

OA

=

a

，

OB

=

b

，

OC

=

c

，且|

a

|=|

b

|=|

c

|=1，则∠AOB=∠BOC=∠AOC=

π

3

，

a

•

b

=

b

•

c

=

c

•

a

=

1

2

，由此能求出异面直线OE与BF所成角的余弦值．

解答： 解：如图所示，设

OA

=

a

，

OB

=

b

，

OC

=

c

，
且|

a

|=|

b

|=|

c

|=1，
∴∠AOB=∠BOC=∠AOC=

π

3

，
∴

a

•

b

=

b

•

c

=

c

•

a

=

1

2

，
∵

OE

=

1

2

(

OA

+

OB

)=

1

2

(

a

+

b

)，

BF

=

OF

-

OB

=

1

2

OC

-

OB

=

1

2

c

-

b

，
|

OE

|=|

BF

|=

3

2

，
∴

OE

•

BF

=

1

2

(

a

+

b

)•(

1

2

c

-

b

)
=

1

4

a

•

c

+

1

4

b

•

c

-

1

2

a

•

b

-

1

2

b

2=-

1

2

，
∴cos＜

OE

，

BF

＞=

- 1 2

3 2 • 3 2

=-

2

3

．
∴异面直线OE与BF所成角的余弦值为

2

3

．
故选：C．

点评：本题考查异面直线所成角的求法，解题时要认真审题，是中档题，解题时要注意向量法的合理运用．