题目内容
已知函数f(x)=x2-2x+2,x∈[t,t+1]的最小值为g(t)
(1)求函数g(t)的解析式.
(2)若对任意的t,f(x)-m>0在x∈[t,t+1]上恒成立,求m的取值范围.
(1)求函数g(t)的解析式.
(2)若对任意的t,f(x)-m>0在x∈[t,t+1]上恒成立,求m的取值范围.
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)由于函数f(x)=x2-2x+2的图象的对称轴方程为x=1,且x∈[t,t+1],分类讨论求出f(x)的最小值.
(2)由题意可得,函数f(x)的图象恒在直线y=m的上方,根据二次函数的性质可得函数f(x)的最小值
f(1)的值,可得m的范围.
(2)由题意可得,函数f(x)的图象恒在直线y=m的上方,根据二次函数的性质可得函数f(x)的最小值
f(1)的值,可得m的范围.
解答:
解:(1)由于函数f(x)=x2-2x+2的图象的对称轴方程为x=1,x∈[t,t+1],
当t>1 时,函数f(x)=x2-2x+2在区间[t,t+1]上单调第增,f(x)的最小值为g(t)=f(t)=t2-2t+2.
当1∈[t,t+1]时,即0≤t≤1时,函数f(x)在区间[t,1]上单调第减,在区间[1,t+1]上单调第增,
f(x)的最小值为g(t)=f(1)=1.
当t+1<1,即t<0时,函数f(x)=x2-2x+2在区间[t,t+1]上单调第减,
f(x)的最小值为g(t)=f(t+1)=(t+1)2-2(t+1)+2=t2+1.
综上可得,g(t)=
.
(2)由题意可得,对任意的t,当x∈[t,t+1]时,函数f(x)的图象在直线y=m的上方,
故函数f(x)的图象恒在直线y=m的上方.
根据二次函数的性质可得函数f(x)的最小值为f(1)=1,故有m<1.
当t>1 时,函数f(x)=x2-2x+2在区间[t,t+1]上单调第增,f(x)的最小值为g(t)=f(t)=t2-2t+2.
当1∈[t,t+1]时,即0≤t≤1时,函数f(x)在区间[t,1]上单调第减,在区间[1,t+1]上单调第增,
f(x)的最小值为g(t)=f(1)=1.
当t+1<1,即t<0时,函数f(x)=x2-2x+2在区间[t,t+1]上单调第减,
f(x)的最小值为g(t)=f(t+1)=(t+1)2-2(t+1)+2=t2+1.
综上可得,g(t)=
|
(2)由题意可得,对任意的t,当x∈[t,t+1]时,函数f(x)的图象在直线y=m的上方,
故函数f(x)的图象恒在直线y=m的上方.
根据二次函数的性质可得函数f(x)的最小值为f(1)=1,故有m<1.
点评:本题主要考查对数函数、二次函数的性质,复合函数的单调性,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
函数y=x+
(x>0))的最小值为6,则正数a的值为( )
| a |
| x |
| A、1 | B、4 | C、9 | D、16 |
命题“存在x∈R,使2x+x2≤1”的否定是( )
| A、对任意x∈R,有2x+x2>1 |
| B、对任意x∈R,有2x+x2≤1 |
| C、存在x∈R,使2x+x2>1 |
| D、不存在x∈R,使2x+x2≤1 |
设集合A={x|x2-2x=0},B={x|y=
,x∈N},则A∩B=( )
| x+1 |
| A、{0,1,2} |
| B、{0,-1,2} |
| C、{0,2} |
| D、{0} |
已知a,b,c是直线,α,β是平面,下列条件中,能得出直线a⊥平面α的是( )
| A、a⊥c,a⊥b,其中b?α,c?α |
| B、a⊥b,b∥α |
| C、α⊥β,a∥β |
| D、a∥b,b⊥α |
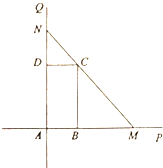 如图,互相垂直的两条公路AP,AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=10m,AD=20m,记三角形花园AMN的面积为S,
如图,互相垂直的两条公路AP,AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=10m,AD=20m,记三角形花园AMN的面积为S,