题目内容
17．已知菱形ABCD的边长为2，∠ABC=60°，则$\overrightarrow{BD}$•$\overrightarrow{CD}$=6．分析 根据菱形中的边角关系，利用余弦定理和数量积公式，即可求出结果．
解答 解：如图所示，
菱形ABCD的边长为2，∠ABC=60°，
∴∠C=120°，
∴BD2=22+22-2×2×2×cos120°=12，
∴BD=2$\sqrt{3}$，
且∠BDC=30°，
∴$\overrightarrow{BD}$•$\overrightarrow{CD}$=|$\overrightarrow{BD}$|×|$\overrightarrow{CD}$|×cos30°=2$\sqrt{3}$×2×$\frac{\sqrt{3}}{2}$=6．
故答案为：6．
点评 本题考查了平面向量的数量积和余弦定理的应用问题，是基础题目．
练习册系列答案
相关题目
7．双曲线$\frac{x^2}{m}-{y^2}=1$的虚轴长是实轴长的2倍，则m=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{1}{4}$ |
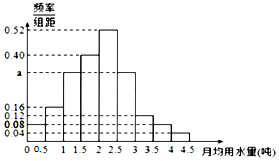我国是世界上严重缺水的国家，某市政府为了鼓励全市30万居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超过x的部分按议价收费，并希望约80%的居民每月的用水量不超过标准x（吨）．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），[4，4.5）分成9组，制成了如图所示的频率分布直方图．
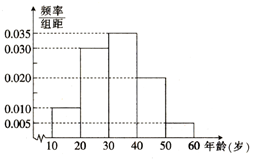随着医院对看病挂号的改革，网上预约成为了当前最热门的就诊方式，这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题；某医院研究人员对其所在地区年龄在10～60岁间的n位市民对网上预约挂号的了解情况作出调查，并将被调查的人员的年龄情况绘制成频率分布直方图，如右图所示．