题目内容
7.双曲线$\frac{x^2}{m}-{y^2}=1$的虚轴长是实轴长的2倍,则m=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{4}$ |
分析 根据题意,有双曲线的方程分析可得其焦点在x轴上以及a、b的值,进而可得该双曲线的实轴、虚轴长,结合题意可得2=2×2$\sqrt{m}$,解可得m的值,即可得答案.
解答 解:根据题意,双曲线的方程为$\frac{x^2}{m}-{y^2}=1$,
则其焦点在x轴上,且a=$\sqrt{m}$,b=1,
故其虚轴长2b=2,实轴长2a=2$\sqrt{m}$,
又由该双曲线的虚轴长是实轴长的2倍,则有2=2×2$\sqrt{m}$,
解可得m=$\frac{1}{4}$;
故选:A.
点评 本题考查双曲线的几何性质,关键是利用双曲线的标准方程求出实轴、虚轴长.

练习册系列答案
相关题目
15.如表提供了某厂节能降耗技术改造后在生产A产品过程中纪录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据:
根据上表提供的数据,求得y关于x的线性回归方程为$\widehat{y}$=0.7x+0.35,那么表中n的值为( )注($\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$)
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | n | 4 | 4.5 |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
2.已知直线l1:y=-1和直线l2:3x-4y+19=0,抛物线x2=4y上一动点P到直线l1和直线l2的距离之和最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{24}{5}$ | D. | $\frac{5}{2}$ |
19.设全集U={1,2,3,4,5,6,7,8},集合A={1,2,3,5},B={2,4,6},则B∩∁UA=( )
| A. | {2} | B. | {4,6} | C. | {1,3,5} | D. | {4,6,7,8} |
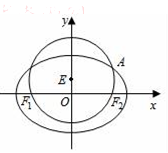 已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.
已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.