题目内容
已知二次函数f(x)同时满足①f(0)=f(2),②f(x)max=15,③方程f(x)=0的两根的立方和等于17.(立方和公式:a3+b3=(a+b)(a2-ab+b2))
(1)求f(x)的解析式.
(2)求函数f(x)在区间[-1,2]上的值域.
(1)求f(x)的解析式.
(2)求函数f(x)在区间[-1,2]上的值域.
考点:函数的值域,二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)由题目条件设f(x)=a(x-1)2+15(a≠0),从而解解析式;
(2)由单调性求值域.
(2)由单调性求值域.
解答:
解:(1)∵f(0)=f(2)∴对称轴为直线x=1;
依题意设f(x)=a(x-1)2+15(a≠0),方程f(x)=0的根为x1和x2;
则x1+x2=2,x1x2=
;
∴
+
=(x1+x2)(
-x1x2+
)=(x1+x2)[(x1+x2)2-3x1x2]
=2(4-3•
)=17;
解得,a=-6.
∴f(x)=-6(x-1)2+15=-6x2+12x+9.
(2)∵f(x)的图象开口向下,对称轴为直线x=-1,又∵x∈[-1,2];
∴当x=1时,f(x)有最大值15.
当x=-1时,f(x)有最小值-9.
故f(x)的值域为[-9,15].
依题意设f(x)=a(x-1)2+15(a≠0),方程f(x)=0的根为x1和x2;
则x1+x2=2,x1x2=
| a+15 |
| a |
∴
| x | 3 1 |
| x | 3 2 |
| x | 2 1 |
| x | 2 2 |
=2(4-3•
| a+15 |
| a |
解得,a=-6.
∴f(x)=-6(x-1)2+15=-6x2+12x+9.
(2)∵f(x)的图象开口向下,对称轴为直线x=-1,又∵x∈[-1,2];
∴当x=1时,f(x)有最大值15.
当x=-1时,f(x)有最小值-9.
故f(x)的值域为[-9,15].
点评:本题考查了二次函数的性质,是高考的重点,要求学生熟练应用二次函数的性质解题.

练习册系列答案
相关题目
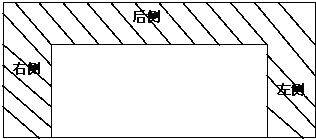 某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?
某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?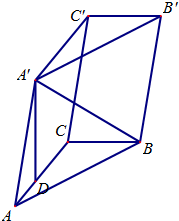 如图,三棱柱ABC-A′B′C′中,点A′在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC′=2.
如图,三棱柱ABC-A′B′C′中,点A′在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC′=2.