题目内容
(1)已知正三棱锥V-ABC的正视图、侧视图和俯视图如图1.求侧视图的面积.
(2)已知某几何体的三视图如图2,当a+b取最大值时,求这个几何体的体积.
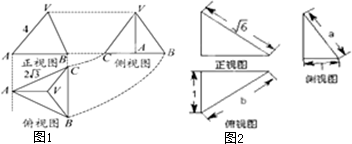
(2)已知某几何体的三视图如图2,当a+b取最大值时,求这个几何体的体积.

考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:(1)由题意可知,应求底面边长与体高;(2)设出高与长,求最大值时的高与长,从而求体积.
解答:
解:(1)由图知,正三棱锥V-ABC底面边长为2
;
底面的高为2
×
=3,
则正三棱锥V-ABC的体高为
=2
,
则侧视图的面积S=
×2
×2
=6.
(2)设三视图的长为经x,高为y;
则1+x2=b2,x2+y2=
2,1+y2=a2;
则b2-1+a2-1=6;
即a2+b2=8;
则当a=b=2时,a+b取得最大值.
此时,x=y=
.
则这个几何体的体积V=
•(
•
•1)•
=
.
| 3 |
底面的高为2
| 3 |
| ||
| 2 |
则正三棱锥V-ABC的体高为
42-(3×
|
| 3 |
则侧视图的面积S=
| 1 |
| 2 |
| 3 |
| 3 |
(2)设三视图的长为经x,高为y;
则1+x2=b2,x2+y2=
| 6 |
则b2-1+a2-1=6;
即a2+b2=8;
则当a=b=2时,a+b取得最大值.
此时,x=y=
| 3 |
则这个几何体的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
点评:本题考查了学生的空间想象力及三视图中量的相等关系,属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 一个长、宽分别为
一个长、宽分别为| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
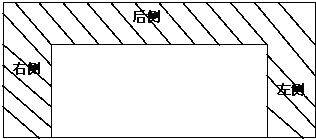 某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?
某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?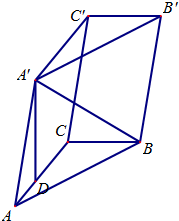 如图,三棱柱ABC-A′B′C′中,点A′在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC′=2.
如图,三棱柱ABC-A′B′C′中,点A′在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC′=2.