题目内容
已知函数f（x）=-x2+2ax-1，若f（x）在[-1，1]上的最大值为g（a），求g（a）的解析式．
考点：函数的最值及其几何意义,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：先对解析式配方，确定函数的对称轴，由于只求最大值，根据对称轴与区间的位置关系分三种情形讨论，最后用分段函数形式表示出函数的最大值．
解答：
解：由题意得，f（x）=-（x-a）2+a2-1，
①当a≤-1时，f（x）在[-1，1]上单调减，
∴f（x）max=f（-1）=-2a-2，
②当-1＜a＜1时，f（x）在[-1，a]上单调增，在（a，1]上单调，
∴f(x)max=f(a)=a2-1，
③当a≥1时，f（x）在[-1，1]上单调增，
∴f（x）max=f（1）=2a-2，
综上得，g(a)=
．
①当a≤-1时，f（x）在[-1，1]上单调减，
∴f（x）max=f（-1）=-2a-2，
②当-1＜a＜1时，f（x）在[-1，a]上单调增，在（a，1]上单调，
∴f(x)max=f(a)=a2-1，
③当a≥1时，f（x）在[-1，1]上单调增，
∴f（x）max=f（1）=2a-2，
综上得，g(a)=
|
点评：本题考查了二次函数的图象和性质，特别是求二次函数的最值，需要分类讨论，做到不重不漏，解题时要学会用数形结合的思想方法解决问题．
练习册系列答案
相关题目
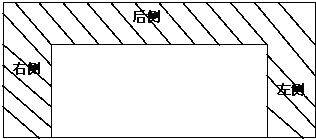某村计划建造一个室内面积为72m2的矩形蔬菜温室．在温室内沿左、右两侧与后侧内墙各保留1m宽的通道，当矩形温室的边长各为多少时？蔬菜的种植面积最大，最大种植面积是多少？
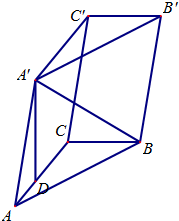如图，三棱柱ABC-A′B′C′中，点A′在平面ABC内的射影D在AC上，∠ACB=90°，BC=1，AC=CC′=2．