题目内容
已知函数f(x)=
(I)判断f(x)的奇偶性;
(Ⅱ)确定函数f(x)在(-∞,0)上是增函数还是减函数?证明你的结论.
(Ⅲ)若对任意x∈[1,2]都有f(x)≤
-1恒成立,求a的取值范围.
| 1 |
| 1+x2 |
(I)判断f(x)的奇偶性;
(Ⅱ)确定函数f(x)在(-∞,0)上是增函数还是减函数?证明你的结论.
(Ⅲ)若对任意x∈[1,2]都有f(x)≤
| a |
| 2 |
考点:函数奇偶性的判断,函数单调性的性质,函数恒成立问题
专题:函数的性质及应用
分析:(1)根据函数的奇偶性进行判断;
(2)根据增减函数的定义进行判断和证明;
(3)先求出函数的最大值,只要最大值满足就可以了.
(2)根据增减函数的定义进行判断和证明;
(3)先求出函数的最大值,只要最大值满足就可以了.
解答:
解:(I)因为函数为f(x)=
所以定义域为{x|∈R}---------1
f(-x)=
=
=f(x),∴f(x)为偶函数.-----------------3
(Ⅱ)在区间(-∞,0)上取x1,x2且x1<x2,
f(x1)-f(x2)=
-
=
-------------------------4
----------------------6
因为x12+1>0,x12+1>0,且x1<x2,∴x2+x1<0,x2-x1>0-----------8
∴f(x1)-f(x2)<0,所以f(x)在(-∞,0)上为增函数.--------------------10
(Ⅲ)f(x)max=f(1)≤
-1即可,---------------------12
易得a≥3--------------14
| 1 |
| 1+x2 |
f(-x)=
| 1 |
| 1+(-x)2 |
| 1 |
| 1+x2 |
(Ⅱ)在区间(-∞,0)上取x1,x2且x1<x2,
f(x1)-f(x2)=
| 1 |
| 1+x12 |
| 1 |
| 1+x22 |
| (x2-x1)(x2+x1) |
| (x12+1)(x22+1) |
----------------------6
因为x12+1>0,x12+1>0,且x1<x2,∴x2+x1<0,x2-x1>0-----------8
∴f(x1)-f(x2)<0,所以f(x)在(-∞,0)上为增函数.--------------------10
(Ⅲ)f(x)max=f(1)≤
| a |
| 2 |
易得a≥3--------------14
点评:本题主要考查函数的奇偶性和单调性以及恒成立问题,属于中档题.

练习册系列答案
相关题目
已知
(
+
)=2,则a=( )
| lim |
| x→∞ |
| 2 |
| x-1 |
| ax-1 |
| x-1 |
| A、-6 | B、2 | C、3 | D、6 |
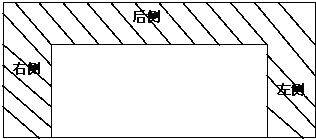 某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?
某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?