题目内容

在△ABC中，角A，B，C的对边分别为a，b，c，且cos2C+3cosC=1，c=
7
，又S△ABC=
3
3
2
．
（Ⅰ）求角C的大小；
（Ⅱ）求sinA+sinB的值．
考点：正弦定理
专题：解三角形
分析：（1）由cos2C+3cosC=1求得cosC的值，从而求得 故C的值．
（2）根据c=
7
，C=
π
3
，S△ABC=
3
3
2
可得
1
2
ab•sinC=
3
3
2
，求得ab的值，再由余弦定理求得a+b的值，从而求得sinA+sinB=
(a+b)sinC
c
 的值．
解答： 解：（1）由cos2C+3cosC=1得，2cos2C+3cosC-2=0，
解得cosC=
1
2
，或cosC=-2（舍去），故C=
π
3
．
（2）∵c=
7
，C=
π
3
，S△ABC=
3
3
2
，∴
1
2
ab•sinC=
3
3
2
，ab=6．
由余弦定理得，c2=（a+b）2-2ab（1+cosC），
又结合（1）及已知得7=（a+b）2-12（1+
1
2
），解得a+b=5．
∴sinA+sinB=
(a+b)sinC
c
=
5×
3
2
7
=
5
21
14
．
点评：本题主要考查二倍角公式、正弦定理、余弦定理的应用，属于中档题．
练习册系列答案
相关题目
如果实数x、y满足
x-y+3≥0
x+y-1≥0
x≤1
，若直线y=k（x-1）将可行域分成面积相等的两部分，则实数k的值为
 
．
有下列四个命题：
①“若A∪B=B，则A?B”；
②“若b≤1，则方程x2-2bx+b2+b=0有实根”的逆否命题；
③“若y=f（x）是奇函数，则f（0）=0”的否命题；
④“若x＞y＞1，则logx3＜logy3”的逆命题．
其中真命题的个数是（　　）
A、0B、1C、2D、3
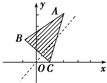在△ABC中，三顶点分别为A（2，4），B（-1，2），C（1，0），点P（x，y）在△ABC内部及其边界上运动，则m=y-x的取值范围为（　　）
A、[1，3]
B、[-3，1]
C、[-1，3]
D、[-3，-1]
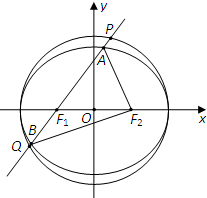已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)和圆O：x2+y2=a2，F1（-1，0），F2（1，0）分别是椭圆的左、右两焦点，过F1且倾斜角为α(α∈(0，
π
2
])的动直线l交椭圆C于A，B两点，交圆O于P，Q两点（如图所示，
点A在轴上方）．当α=
π
4
时，弦PQ的长为
14
．
（1）求圆O和椭圆C的方程；
（2）若点M是椭圆C上一点，求当AF2，BF2，AB成等差数列时，△MPQ面积的最大值．
若变量x，y满足约束条件
y≤1
x+y≥0
x-y-2≤0
，建立直角坐标系，画出不等式组表示的平面区域，求z=x-2y的最大值并求出取得最值时的最优解的坐标．
已知椭圆C的中心在原点，焦点在x轴上，以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形，直线l：y=x+m与轨迹C交于不同的两点P和Q．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在常数m，使
OP
•
OQ
=0？若存在，求出m的值；若不存在，请说明理由．
已知
AB
=(2，5)，
AC
=(3，4)，
AD
=(1，6)，且
AC
=α
AB
+β
AD
，求α，β的值．
设P为函数f（x）=sinπx的图象上的一个最高点，Q为函数g（x）=cosπx的图象上的一个最低点，则|PQ|最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网