题目内容
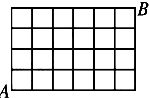 某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )
某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )| A、m=90,n=210 |
| B、m=210,n=210 |
| C、m=210,n=792 |
| D、m=90,n=792 |
考点:组合及组合数公式
专题:排列组合
分析:(1)在7条竖线中任选2条,5条横线中任选2条,这样4条线即可组成一个矩形;(2)每种最短走法,即是从10段中选出6段走东向的,选出4段走北向的,由组合数和计数原理可得.
解答:
解:(1)在7条竖线中任选2条,5条横线中任选2条,这样4条线即可组成一个矩形,
故可组成的矩形有
•
=210(个).
(2)每条东西向的街道被分成六段,每条南北向的街道被分成4段,
从A到B最短的走法,无论怎样走,一定包括10段,其中6段方向相同,另4段方向相同,
每种最短走法,即是从10段中选出6段走东向的,选出4段走北向的,
故共有
=
=210种走法.
故选:B
故可组成的矩形有
| C | 2 7 |
| C | 2 5 |
(2)每条东西向的街道被分成六段,每条南北向的街道被分成4段,
从A到B最短的走法,无论怎样走,一定包括10段,其中6段方向相同,另4段方向相同,
每种最短走法,即是从10段中选出6段走东向的,选出4段走北向的,
故共有
| C | 6 10 |
| C | 4 4 |
| C | 4 10 |
故选:B
点评:本题考查排列组合的简单应用,得出组成矩形的条件和最短走法是解决问题的关键,属基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
直线x=ky+3与双曲线
-
=1只有一个公共点,则k的值有( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、1个 | B、2个 |
| C、3个 | D、无数多个 |
“2a>2b”是“lga>lgb”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
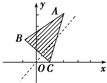 在△ABC中,三顶点分别为A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC内部及其边界上运动,则m=y-x的取值范围为( )
在△ABC中,三顶点分别为A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC内部及其边界上运动,则m=y-x的取值范围为( )| A、[1,3] |
| B、[-3,1] |
| C、[-1,3] |
| D、[-3,-1] |