题目内容
18.已知?x∈(0,+∞),[(m-1)x-1](x2-mx-1)≥0恒成立,则m的值为$\frac{3}{2}$.分析 对m≤1和m>1分类,若m≤1,由x>0,可得(m-1)x-1<0,而y=x2-mx-1的图象开口向上,可知[(m-1)x-1](x2-mx-1)≥0不恒成立,因此m>1,由(m-1)x-1=0,解得x=$\frac{1}{m-1}$>0,而方程x2-mx-1=0的两个实数根异号,x=$\frac{1}{m-1}$必定是方程x2-mx-1=0的一个正根,把x=$\frac{1}{m-1}$代入方程x2-mx-1=0,求解可得m的值.
解答 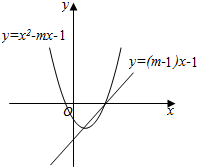 解:若m≤1,∵x>0,∴(m-1)x-1<0,
解:若m≤1,∵x>0,∴(m-1)x-1<0,
又y=x2-mx-1的图象开口向上,
∴[(m-1)x-1](x2-mx-1)≥0不恒成立,
因此m>1,如图:
由(m-1)x-1=0,解得x=$\frac{1}{m-1}$>0,而方程x2-mx-1的两个实数根异号,
要使?x∈(0,+∞),[(m-1)x-1](x2-mx-1)≥0恒成立,
∴x=$\frac{1}{m-1}$必定是方程x2-mx-1的一个正根,
把x=$\frac{1}{m-1}$代入方程x2-mx-1可得:$(\frac{1}{m-1})^{2}-\frac{m}{m-1}-1=0$,
又m>1,解得m=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查恒成立问题,考查了二次函数的单调性、一元二次方程的解与函数的零点,关键是掌握等价转化方法,考查了推理能力和计算能力,将条件转化为方程(m-1)x-1=0与x2-mx-1=0在(0,+∞)上有相同零点是解决本题的关键,综合性强,难度较大.

练习册系列答案
相关题目
10.过点A(4,-a)和点B(6,b)的直线与直线y=-x+m垂直,则以AB为直径的圆的方程可以是( )
| A. | x2+y2-10x+17=0 | B. | x2+y2-2y-1=0 | ||
| C. | x2+y2-8x-4y+12=0 | D. | x2+y2-10x-2y+24=0 |