题目内容
7.一个三角形在其直观图中对应一个边长为2的正三角形,原三角形的面积为2$\sqrt{6}$.分析 求出边长为2的正三角形的面积,再利用原图与直观图的面积比求出对应的体积即可.
解答 解:∵三角形的直观图是一个边长为2正三角形,
∴S直观图=$\frac{1}{2}$×22×sin60°=$\sqrt{3}$,
又S原图=S直观图•2$\sqrt{2}$=$\sqrt{3}$×2$\sqrt{2}$=2$\sqrt{6}$.
故答案为:2$\sqrt{6}$.
点评 本题考查了直观图的应用问题,解题时应了解原图面积与直观图面积的关系是多少,是基础题目.

练习册系列答案
相关题目
15.已知等比数列{an}的各项均为正数,公比q≠1,设P=$\frac{1}{2}$(${log_{\frac{1}{2}}}{a_5}+{log_{\frac{1}{2}}}{a_7}$),Q=${log_{\frac{1}{2}}}\frac{{{a_3}+{a_9}}}{2}$,则P与Q的大小关系是( )
| A. | P≥Q | B. | P<Q | C. | P≤Q | D. | P>Q |
2.函数f(x)=2sin(ωx+φ)(ω>0,一$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则( )
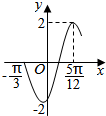
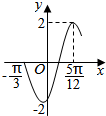
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=一$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |
19.一个圆锥的轴截面为正三角形,其边长为a,则其表面积为( )
| A. | $\frac{5}{4}{a^2}$π | B. | a2π | C. | $\frac{3}{4}{a^2}$π | D. | $\frac{1}{4}{a^2}$π |
16.满足2n-1<(n+1)2的最大正整数n的取值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |