Question

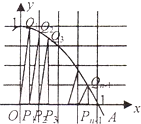如图，记二次函数y=-x²+1的图象与x轴正半轴的交点为A，将线段OA分成n等份．设分点分别为P₁，P₂，…，P_n-1．过每个分点作x轴的垂线，分别与该图象交Q₁，Q₂，…，Q_n-1再记直角三角形OP₁Q₁，P₁P₂Q₂，…的面积分别为S₁，S₂…，这样就有S₁=

n2-1

2n3

，S₂=

n2-4

2n3

，…；记W=S₁+S₂+…+S_n-1，当n越来越大时，W最接近的常数是（　　）

• A、

  1

  2

• B、

  1

  3

• C、

  1

  4

• D、

  2

  3

Answer 1

考点：二次函数的性质

专题：计算题,导数的综合应用

分析：由题意，W=S₁+S₂+…+S_n-1，当n越来越大时，可看成积分．

解答： 解：由题意，W=S₁+S₂+…+S_n-1，当n越来越大时，可看成积分．

1

2

×

∫

1 0

(-x2+1)dx=

1

2

×（-

1

3

+1-0）=

1

3

．
故选B．

点评：本题考查了积分的定义，属于基础题．