题目内容
已知f(x-1)=x2+4x-5,则f(x+1)=( )
| A、x2+6x |
| B、x2+8x+7 |
| C、x2+2x-3 |
| D、x2+6x-10 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:通过已知的f(x-1)解析式求出f(x)的解析式,根据f(x)的解析式即可求得f(x+1)的解析式.
解答:
解:f(x-1)=(x-1)2+6(x-1),∴f(x)=x2+6x;
∴f(x+1)=(x+1)2+6(x+1)=x2+8x+7.
∴f(x+1)=(x+1)2+6(x+1)=x2+8x+7.
点评:考查函数的解析式,以及通过f(x-1)解析式先求出f(x)解析式,再求f(x+1)解析式的方法.

练习册系列答案
相关题目
 如图是一个类似“杨辉三角”的图形,第n行共有n个数,且 该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和,其中an,1,an,2,…,an,n(n=1,2,3,)分别表示第n行的第一个数,第二个数,….第n 个数.则an,2(n≥2且n∈N)的通项公式是( )
如图是一个类似“杨辉三角”的图形,第n行共有n个数,且 该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和,其中an,1,an,2,…,an,n(n=1,2,3,)分别表示第n行的第一个数,第二个数,….第n 个数.则an,2(n≥2且n∈N)的通项公式是( )A、an,2=
| ||
B、an,2=
| ||
C、an,2=
| ||
D、an,2=
|
在《爸爸去哪儿》第二季第四期中,村长给6位“萌娃”布置一项搜寻空投食物的任务.已知:①食物投掷地点有远、近两处; ②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处.则不同的搜寻方案有( )
| A、40种 | B、70种 |
| C、80种 | D、100种 |
已知函数f(x)=asinx+bx3+cx+1(a,b,c∈R),f(lg(lg3))=3,则f(lg(log310))=( )
| A、3 | B、-1 | C、-3 | D、2014 |
已知函数f(x)=
,且方程f(x)=mx+1在区间[-2π,π]内有两个不等的实根,则实数m的取值范围为( )
|
| A、[-4,2] |
| B、(-4,3) |
| C、(-4,2)∪{4} |
| D、[2,4] |
若2x+y≥1,u=y 2-2y+x 2+6x,则u的最小值等于( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
在△ABC中,sinA=sinB是A=B的( )
| A、充要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、既非充分条件又非必要条件 |
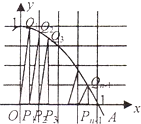 如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=
如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=