题目内容
已知3sinα+4cosα=5,则tanα= .
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:由3sinα+4cosα=5,可得5sin(α+β)=5(tanβ=
),进而可得tanα=tan(2kπ+
-β)=
.
| 4 |
| 3 |
| π |
| 2 |
| 1 |
| tanβ |
解答:
解:∵3sinα+4cosα=5,
∴5sin(α+β)=5(tanβ=
)
∴sin(α+β)=1
∴α=2kπ+
-β,
∴tanα=tan(2kπ+
-β)=
=
.
故答案为:
.
∴5sin(α+β)=5(tanβ=
| 4 |
| 3 |
∴sin(α+β)=1
∴α=2kπ+
| π |
| 2 |
∴tanα=tan(2kπ+
| π |
| 2 |
| 1 |
| tanβ |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查同角三角函数基本关系的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知A=(1,-2),若向量
与
=(2,-3)反向,|
|=4
,则点B的坐标为( )
| AB |
| a |
| AB |
| 3 |
| A、(10,7) |
| B、(-10,7) |
| C、(7,-10) |
| D、(-7,10) |
奇函数f(x)=
(其中a为常数)的定义域为( )
| ||
| x-a |
| A、(-1,0)∪(0,1) |
| B、[-1,0)∪(0,-1] |
| C、[-1,1] |
| D、(-∞,-1][1,+∞) |
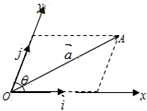 已知单位向量
已知单位向量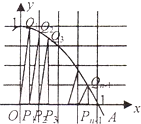 如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=
如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=