题目内容
已知函数f(x)=
,若f(a)+f(1)=0,则实数a的值等于( )
|
| A、-3 | B、-l | C、1 | D、-3或l |
考点:分段函数的应用
专题:函数的性质及应用
分析:根据分段函数的表达式,即可得到结论.
解答:
解:由分段函数的表达式可知f(1)=lg1=0,
则方程f(a)+f(1)=0,
即f(a)=0,
若a>0,则lga=0,解得a=1,
若a≤0.则f(a)=a+3=0,解得a=-3,
综上a=-3或a=1,
故选:D
则方程f(a)+f(1)=0,
即f(a)=0,
若a>0,则lga=0,解得a=1,
若a≤0.则f(a)=a+3=0,解得a=-3,
综上a=-3或a=1,
故选:D
点评:本题主要考查函数值的计算,根据分段函数进行分段求解是解决本题的关键.

练习册系列答案
相关题目
已知A=(1,-2),若向量
与
=(2,-3)反向,|
|=4
,则点B的坐标为( )
| AB |
| a |
| AB |
| 3 |
| A、(10,7) |
| B、(-10,7) |
| C、(7,-10) |
| D、(-7,10) |
奇函数f(x)=
(其中a为常数)的定义域为( )
| ||
| x-a |
| A、(-1,0)∪(0,1) |
| B、[-1,0)∪(0,-1] |
| C、[-1,1] |
| D、(-∞,-1][1,+∞) |
为得到函数y=sin2x的图象,只需将函数y=cos(x+
)的图象( )
| π |
| 3 |
A、横坐标变为原来2倍,再向右平移
| ||||
B、横坐标变为原来2倍,再向右平移
| ||||
C、横坐标变为原来
| ||||
D、横坐标变为原来
|
 如图是一个类似“杨辉三角”的图形,第n行共有n个数,且 该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和,其中an,1,an,2,…,an,n(n=1,2,3,)分别表示第n行的第一个数,第二个数,….第n 个数.则an,2(n≥2且n∈N)的通项公式是( )
如图是一个类似“杨辉三角”的图形,第n行共有n个数,且 该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和,其中an,1,an,2,…,an,n(n=1,2,3,)分别表示第n行的第一个数,第二个数,….第n 个数.则an,2(n≥2且n∈N)的通项公式是( )A、an,2=
| ||
B、an,2=
| ||
C、an,2=
| ||
D、an,2=
|
已知向量
,
满足|
|=1,
=(1,
),且
⊥(
+
),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| a |
| b |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |
函数y=f(x)的部分图象如图所示,则y=f(x)的解析式为( )
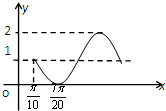

A、y=2sin(2x-
| ||
B、y=sin(2x-
| ||
C、y=2sin(2x+
| ||
D、y=sin(2x+
|
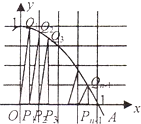 如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=
如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=