题目内容
已知集合A={y|y=-x2-2x},B={x|y=
},且A∪B=R,则实数a的最大值是( )
| x-a |
| A、1 | B、-1 | C、0 | D、2 |
考点:并集及其运算
专题:集合
分析:求出A中y的范围确定出A,求出B中x的范围确定出B,根据A与B的并集为R,确定出a的最大值即可.
解答:
解:由y=-x2-2x=-(x+1)2+1≤1,即A=(-∞,1],
由y=
,得到x≥a,即B=[a,+∞),
∵A∪B=R,
∴画出数轴可知a≤1,
则实数a的最大值是1.

故选:A.
由y=
| x-a |
∵A∪B=R,
∴画出数轴可知a≤1,
则实数a的最大值是1.

故选:A.
点评:此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
为得到函数y=sin2x的图象,只需将函数y=cos(x+
)的图象( )
| π |
| 3 |
A、横坐标变为原来2倍,再向右平移
| ||||
B、横坐标变为原来2倍,再向右平移
| ||||
C、横坐标变为原来
| ||||
D、横坐标变为原来
|
已知向量
,
满足|
|=1,
=(1,
),且
⊥(
+
),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| a |
| b |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |
已知数列{an}中,a2=7,且an=an+1-6(n∈N*),则前n项和Sn=( )
A、
| ||
| B、n2 | ||
C、
| ||
| D、3n2-2n |
已知a,b,c,d∈R,则下列选项正确的是( )
| A、a>b⇒am2>bm2 | ||||
B、
| ||||
| C、a>b,c>d⇒a+c>b+d | ||||
D、a>b⇒
|
设{an}是各项互不相等的正数等差数列,{bn}是各项互不相等的正数等比数列,a1=b1,a2n+1=b2n+1,则( )
| A、an+1>bn+1 |
| B、an+1≥bn+1 |
| C、an+1<bn+1 |
| D、an+1=bn+1 |
在公差为4的正项等差数列中,a3与2的算术平均值等于S3与2的几何平均值,其中S3 表示数列的前三项和,则a10为( )
| A、38 | B、40 | C、42 | D、44 |
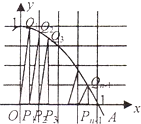 如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=
如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=