题目内容
设α表示平面,a,b表示直线,给出下列四个命题:
①a∥α,a⊥b⇒b∥α;
②a∥b,a⊥α⇒b⊥α;
③a⊥α,a⊥b⇒b?α;
④a⊥α,b⊥α⇒a∥b.
其中正确命题的序号是( )
①a∥α,a⊥b⇒b∥α;
②a∥b,a⊥α⇒b⊥α;
③a⊥α,a⊥b⇒b?α;
④a⊥α,b⊥α⇒a∥b.
其中正确命题的序号是( )
| A、①② | B、②④ | C、③④ | D、①③ |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①a∥α,a⊥b⇒b与α平行,相交或b?α,故①错误;
②若a∥b,a⊥α,由收直线与平面垂直和判定定理得b⊥α,故②正确;
③a⊥α,a⊥b⇒b与α平行,相交或b?α,故③错误;
④若a⊥α,b⊥α,则由直线与平面垂直的性质得a∥b,故④正确.
故选:B.
②若a∥b,a⊥α,由收直线与平面垂直和判定定理得b⊥α,故②正确;
③a⊥α,a⊥b⇒b与α平行,相交或b?α,故③错误;
④若a⊥α,b⊥α,则由直线与平面垂直的性质得a∥b,故④正确.
故选:B.
点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
已知A=(1,-2),若向量
与
=(2,-3)反向,|
|=4
,则点B的坐标为( )
| AB |
| a |
| AB |
| 3 |
| A、(10,7) |
| B、(-10,7) |
| C、(7,-10) |
| D、(-7,10) |
已知向量
,
满足|
|=1,
=(1,
),且
⊥(
+
),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| a |
| b |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |
已知a,b,c,d∈R,则下列选项正确的是( )
| A、a>b⇒am2>bm2 | ||||
B、
| ||||
| C、a>b,c>d⇒a+c>b+d | ||||
D、a>b⇒
|
已知函数f(x)=
,且方程f(x)=mx+1在区间[-2π,π]内有两个不等的实根,则实数m的取值范围为( )
|
| A、[-4,2] |
| B、(-4,3) |
| C、(-4,2)∪{4} |
| D、[2,4] |
设{an}是各项互不相等的正数等差数列,{bn}是各项互不相等的正数等比数列,a1=b1,a2n+1=b2n+1,则( )
| A、an+1>bn+1 |
| B、an+1≥bn+1 |
| C、an+1<bn+1 |
| D、an+1=bn+1 |
函数y=f(x)的部分图象如图所示,则y=f(x)的解析式为( )
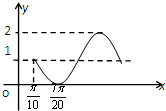

A、y=2sin(2x-
| ||
B、y=sin(2x-
| ||
C、y=2sin(2x+
| ||
D、y=sin(2x+
|
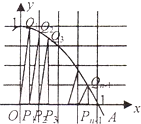 如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=
如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=