题目内容
已知直线l1:y=2x+1,l2:y=2x+5,则直线l1与l2的位置关系是( )
| A、重合 | B、垂直 |
| C、相交但不垂直 | D、平行 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:利用斜率存在的两条直线平行的充要条件即可判断出.
解答:
解:由直线l1:y=2x+1,l2:y=2x+5,
可得斜率都等于2,截距不相等.
∴l1∥l2.
故选:D.
可得斜率都等于2,截距不相等.
∴l1∥l2.
故选:D.
点评:本题考查了斜率存在的两条直线平行的充要条件、斜截式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
奇函数f(x)=
(其中a为常数)的定义域为( )
| ||
| x-a |
| A、(-1,0)∪(0,1) |
| B、[-1,0)∪(0,-1] |
| C、[-1,1] |
| D、(-∞,-1][1,+∞) |
已知函数f(x)=
,且方程f(x)=mx+1在区间[-2π,π]内有两个不等的实根,则实数m的取值范围为( )
|
| A、[-4,2] |
| B、(-4,3) |
| C、(-4,2)∪{4} |
| D、[2,4] |
设{an}是各项互不相等的正数等差数列,{bn}是各项互不相等的正数等比数列,a1=b1,a2n+1=b2n+1,则( )
| A、an+1>bn+1 |
| B、an+1≥bn+1 |
| C、an+1<bn+1 |
| D、an+1=bn+1 |
若2x+y≥1,u=y 2-2y+x 2+6x,则u的最小值等于( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
函数y=f(x)的部分图象如图所示,则y=f(x)的解析式为( )
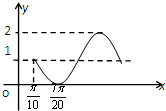

A、y=2sin(2x-
| ||
B、y=sin(2x-
| ||
C、y=2sin(2x+
| ||
D、y=sin(2x+
|
若正方形ABCD的面积为2,且
=
,
=
,
=
,则|
+
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
| B、2 | ||
| C、4 | ||
D、3
|
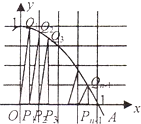 如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=
如图,记二次函数y=-x2+1的图象与x轴正半轴的交点为A,将线段OA分成n等份.设分点分别为P1,P2,…,Pn-1.过每个分点作x轴的垂线,分别与该图象交Q1,Q2,…,Qn-1再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2…,这样就有S1=