题目内容
设a+b+c=1，a，b，c∈R+证明：
（1）ab+bc+ca≤
；
（2）
+
+
≥1．
（1）ab+bc+ca≤
| 1 |
| 3 |
（2）
| b2 |
| a |
| c2 |
| b |
| a2 |
| c |
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：利用基本不等式，即可证明．
解答：
证明：（1）∵（a-b）2+（b-c）2+（c-a）2≥0，
∴2（a2+b2+c2）≥2（ab+bc+ca），
∴a2+b2+c2≥ab+bc+ca，
∴（a+b+c）2≥3（ab+bc+ca），
∴ab+bc+ca≤
；
（2）
+a≥2b，
+b≥2c，
+c≥2a，三式相加(
+a)+(
+b)+(
+c)≥2(b+c+a)，
∴
+
+
≥a+b+c=1．
∴2（a2+b2+c2）≥2（ab+bc+ca），
∴a2+b2+c2≥ab+bc+ca，
∴（a+b+c）2≥3（ab+bc+ca），
∴ab+bc+ca≤
| 1 |
| 3 |
（2）
| b2 |
| a |
| c2 |
| b |
| a2 |
| c |
| b2 |
| a |
| c2 |
| b |
| a2 |
| c |
∴
| b2 |
| a |
| c2 |
| b |
| a2 |
| c |
点评：本题考查不等式的证明，考查基本不等式的运用，属于中档题．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
过两点A（3，0），B（0，2）的直线方程为（ ）
| A、2x+3y-6=0 |
| B、2x+3y+6=0 |
| C、3x-2y-5=0 |
| D、3x-2y+5=0 |
已知数列{an}中，a1=1，以后各项由公式a1•a2•a3…an=n2，则a3+a5=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知四个函数：①y=f1（x）②y=f2（x）③y=f3（x）④y=f4（x）的图象分别如图所示，则下列等式成立的是（ ）
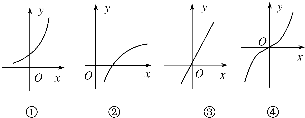
| A、f1（x1+x2）=f1（x1）+f1（x2） |
| B、f2（x1+x2）=f2（x1）+f2（x2） |
| C、f3（x1+x2）=f3（x1）+f3（x2） |
| D、f4（x1+x2）=f4（x1）+f4（x2） |