题目内容
设A是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸缩变换所对应的变换矩阵;B是将点(2,0)变为点(
,1)的旋转变换所对应的变换矩阵;若M=AB;求矩阵M及M-1.
| 3 |
考点:伸缩变换
专题:计算题,矩阵和变换
分析:设矩阵B=
,代入可得
=
,从而求出B=
,进而求M即M-1.
|
|
|
|
|
解答:
解:设矩阵B=
,
则
=
,
则
,
解得,B=
.
又A=
,
则M=AB=
=
.
∵|M|=6≠0,
∴M-1=
.
|
则
|
|
|
则
|
解得,B=
|
又A=
|
则M=AB=
|
|
|
∵|M|=6≠0,
∴M-1=
|
点评:本题考查了矩阵的运算,属于基础题.

练习册系列答案
相关题目
过两点A(3,0),B(0,2)的直线方程为( )
| A、2x+3y-6=0 |
| B、2x+3y+6=0 |
| C、3x-2y-5=0 |
| D、3x-2y+5=0 |
已知四个函数:①y=f1(x)②y=f2(x)③y=f3(x)④y=f4(x)的图象分别如图所示,则下列等式成立的是( )
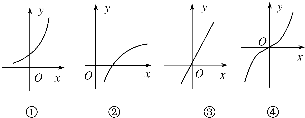

| A、f1(x1+x2)=f1(x1)+f1(x2) |
| B、f2(x1+x2)=f2(x1)+f2(x2) |
| C、f3(x1+x2)=f3(x1)+f3(x2) |
| D、f4(x1+x2)=f4(x1)+f4(x2) |
下列说法正确的个数是( )
①平行于同一直线的两条直线平行
②平行于同一平面的两个平面平行
③两条平行线中的一条和一个平面平行,则另一条也与这个平面平行
④一条直线与两个平行平面中的一个平面平行,则这条直线与另一平面也平行.
①平行于同一直线的两条直线平行
②平行于同一平面的两个平面平行
③两条平行线中的一条和一个平面平行,则另一条也与这个平面平行
④一条直线与两个平行平面中的一个平面平行,则这条直线与另一平面也平行.
| A、1 | B、2 | C、3 | D、4 |
在平面直角坐标系xOy上的区域D由不等式|x+2|+|y+2|≤2给定.则区域D的面积等于( )
| A、2 | ||
| B、4 | ||
C、4
| ||
| D、8 |
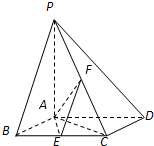 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.