题目内容
已知函数f(x)=exsinx
(1)求函数f(x)的单调区间;
(2)当x∈[0,
]时,f(x)≥kx,求实数k的取值范围.
(1)求函数f(x)的单调区间;
(2)当x∈[0,
| π |
| 2 |
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:导数的综合应用
分析:(1)f′(x)=exsinx+excosx=
exsin(x+
),分别解出f′(x)>0,f′(x)<0,即可得出单调区间;
(2)令g(x)=f(x)-kx=exsinx-kx,即g(x)≥0恒成立,而g′(x)=ex(sinx+cosx)-k,令h(x)=ex(sinx+cosx),利用导数研究函数h(x)的单调性可得:在[0,
]上单调递增,1≤h(x)≤e
,对k分类讨论,即可得出函数g(x)的单调性,进而得出k的取值范围.
| 2 |
| π |
| 4 |
(2)令g(x)=f(x)-kx=exsinx-kx,即g(x)≥0恒成立,而g′(x)=ex(sinx+cosx)-k,令h(x)=ex(sinx+cosx),利用导数研究函数h(x)的单调性可得:在[0,
| π |
| 2 |
| π |
| 2 |
解答:
解:(1)f′(x)=exsinx+excosx=
exsin(x+
),
当x∈(2kπ-
,2kπ+
)时,f′(x)>0,函数f(x)单调递增,
x∈(2kπ+
,2kπ+
),f′(x)<0,函数f(x)单调递减.
(2)令g(x)=f(x)-kx=exsinx-kx,即g(x)≥0恒成立,
而g′(x)=ex(sinx+cosx)-k,
令h(x)=ex(sinx+cosx),h′(x)=ex(sinx+cosx)+ex(cosx-sinx)=2excosx.
∵x∈[0,
],h′(x)≥0,∴h(x)在[0,
]上单调递增,1≤h(x)≤e
,
当k≤1时,g′(x)≥0,g(x)在[0,
]上单调递增,g(x)≥g(0)=0,符合题意;
当k≥e
时,g′(x)≤0,g(x)在[0,
]上单调递减,g(x)≤g(0),与题意不合;
当1<k<e
时,g′(x)为一个单调递增的函数,而g′(0)=1-k<0,g′(
)=e
-k>0,
由零点存在性定理,必存在一个零点x0,使得g′(x0)=0,
当x∈[0,x0)时,g′(x)≤0,从而g(x)在此区间上单调递减,从而g(x)≤g(0)=0,与题意不合,
综上所述:k的取值范围为(-∞,1].
| 2 |
| π |
| 4 |
当x∈(2kπ-
| π |
| 4 |
| 3π |
| 4 |
x∈(2kπ+
| 3π |
| 4 |
| 7π |
| 4 |
(2)令g(x)=f(x)-kx=exsinx-kx,即g(x)≥0恒成立,
而g′(x)=ex(sinx+cosx)-k,
令h(x)=ex(sinx+cosx),h′(x)=ex(sinx+cosx)+ex(cosx-sinx)=2excosx.
∵x∈[0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
当k≤1时,g′(x)≥0,g(x)在[0,
| π |
| 2 |
当k≥e
| π |
| 2 |
| π |
| 2 |
当1<k<e
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
由零点存在性定理,必存在一个零点x0,使得g′(x0)=0,
当x∈[0,x0)时,g′(x)≤0,从而g(x)在此区间上单调递减,从而g(x)≤g(0)=0,与题意不合,
综上所述:k的取值范围为(-∞,1].
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
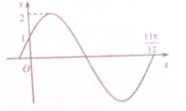
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的图象的第一部分如图所示,则( )
| π |
| 2 |

| A、f(x)的最小正周期为2π | ||
B、f(x)的图象关于直线x=
| ||
C、f(x)的图线关于点(
| ||
D、f(x)在[0,
|
下列命题正确的是( )
| A、直线a与平面α不平行,则a与平面α内的所有直线都不平行 |
| B、直线a与平面α不垂直,则a与平面α内的所有直线都不垂直 |
| C、异面直线a,b不垂直,则过a的任何平面与b都不垂直 |
| D、若直线a和b共面,直线b和c共面,则a和c共面 |
已知等差数列{an}共有2n-1项,则其奇数项之和与偶数项之和的比为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)满足2f(x)+f(-x)=3x+2,则f(2)=( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
