题目内容
已知8个非零实数a1,a2,a3,…,a8,向量
=(a1,a2),
=(a3,a4),
=(a5,a6),
=(a7,a8),对于下列命题:
①a1,a2,a3,…,a8为等差数列,则存在i,j(1≤i,j≤8,i≠j,i,j∈N*),使
与向量
=(ai,aj)共线;
②若a1,a2,a3,…,a8为公差不为0的等差数列,
=(ai,aj)(i≠j,i,j∈N*,1≤i,j≤8),
=(1,1),M={y|y=
•
},则集合M中元素有13个;
③若a1,a2,a3,…,a8为等比数列,则对任意i,j(1≤i,j≤4,i,j∈N*),都有
∥
;
④若a1,a2,a3,…,a8为等比数列,则存在i,j(1≤i,j≤4,i,j∈N*),使
•
<0;
⑤若
=
•
(i≠j,1≤i,j≤4,i,j∈N*),则
的值中至少有一个不小于0.
上述命题正确的是 (填上所有正确命题的序号)
| OA1 |
| OA2 |
| OA3 |
| OA4 |
①a1,a2,a3,…,a8为等差数列,则存在i,j(1≤i,j≤8,i≠j,i,j∈N*),使
| 4 |
 |
| k=1 |
| OAk |
| n |
②若a1,a2,a3,…,a8为公差不为0的等差数列,
| n |
| q |
| n |
| q |
③若a1,a2,a3,…,a8为等比数列,则对任意i,j(1≤i,j≤4,i,j∈N*),都有
| OAi |
| OAj |
④若a1,a2,a3,…,a8为等比数列,则存在i,j(1≤i,j≤4,i,j∈N*),使
| OAi |
| OAj |
⑤若
| m |
| OAi |
| OAj |
| m |
上述命题正确的是
考点:等差数列的性质,等比数列的性质,平面向量数量积的运算
专题:综合题,等差数列与等比数列
分析:利用定义,结合数量积运算,即可得出结论.
解答:
解:①
=(a1+a3+a5+a7,a2+a4+a6+a8)=4(a4,a5),即
与向量(a4,a5)共线,正确;
②∵
=(1,1),M={y|y=
•
},∴y=ai+aj,
不妨设a1,a2,a3,…,a8为1,2,3,4,5,6,7,8,则ai+aj为3,4,5,6,7,8,9,10,11,12,13,14,15,即集合M中元素有13个,正确;
③若a1,a2,a3,…,a8为等比数列,由于
=(a1,a2),
=(a3,a4),
=(a5,a6),
=(a7,a8),所以横、纵坐标都成等比数列,所以都有
∥
,正确;
④若a1,a2,a3,…,a8为等比数列,利用等比数列的性质,可得不存在i,j(1≤i,j≤4,i,j∈N*),使
•
<0;
⑤由8个非零实数a1,a2,a3,…,a8,其中两个的积的和可以都小于0,故不正确.
故答案为:①②③.
| 4 |
 |
| k=1 |
| OAk |
| 4 |
 |
| k=1 |
| OAk |
②∵
| q |
| n |
| q |
不妨设a1,a2,a3,…,a8为1,2,3,4,5,6,7,8,则ai+aj为3,4,5,6,7,8,9,10,11,12,13,14,15,即集合M中元素有13个,正确;
③若a1,a2,a3,…,a8为等比数列,由于
| OA1 |
| OA2 |
| OA3 |
| OA4 |
| OAi |
| OAj |
④若a1,a2,a3,…,a8为等比数列,利用等比数列的性质,可得不存在i,j(1≤i,j≤4,i,j∈N*),使
| OAi |
| OAj |
⑤由8个非零实数a1,a2,a3,…,a8,其中两个的积的和可以都小于0,故不正确.
故答案为:①②③.
点评:本题考查等差数列、等比数列的性质,考查数量积运算,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
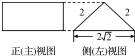 如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8
如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8| 2 |
A、20+8
| ||
B、24+8
| ||
| C、8 | ||
| D、16 |
命题“?a,b∈R,如果a=b,则a2=ab”的否命题为( )
| A、?a,b∈R,如果a2=ab,则a=b |
| B、?a,b∈R,如果a2=ab,则a≠b |
| C、?a,b∈R,如果a2≠ab,则a≠b |
| D、?a,b∈R,如果a≠b,则a2≠ab |
直线x-
y+3=0的斜率是( )
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|