题目内容
13.已知α∈($\frac{π}{2}$,π),sinα=$\frac{\sqrt{5}}{5}$.(1)求sin($\frac{π}{4}$+α)的值;
(2)(理科)求cos($\frac{5π}{6}$-2α)的值.
(文科)求cos2α+sin2α的值.
分析 (1)利用同角三角函数的基本关系求得cosα的值,再利用两角差的三角公式,求得sin($\frac{π}{4}$+α)的值.
(2)利用二倍角公式求得)cos2α+sin2α 的值.
解答 解:(1)∵α∈($\frac{π}{2}$,π),sinα=$\frac{\sqrt{5}}{5}$,∴cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{2\sqrt{5}}{5}$,
∴sin($\frac{π}{4}$+α)=sin$\frac{π}{4}$cosα+cos$\frac{π}{4}$sinα=$\frac{\sqrt{2}}{2}•(-\frac{2\sqrt{5}}{5})$+$\frac{\sqrt{2}}{2}•\frac{1}{5}$=$\frac{\sqrt{2}-2\sqrt{10}}{10}$.
(2)(理科)cos($\frac{5π}{6}$-2α)=-sin($\frac{π}{3}$-2α)=-sin$\frac{π}{3}$cos2α+cos$\frac{π}{3}$sin2α
=-$\frac{\sqrt{3}}{2}$•(2cos2α-1)+$\frac{1}{2}$•2sinαcosα=-$\frac{\sqrt{3}}{2}$•(2•$\frac{4}{5}$-1)+$\frac{\sqrt{5}}{5}•(-\frac{2\sqrt{5}}{5})$=$\frac{-3\sqrt{3}-10}{10}$=-$\frac{3\sqrt{3}+10}{10}$.
(文科)cos2α+sin2α=(2cos2α-1)+2sinαcosα=(2•$\frac{4}{5}$-1)+2•$\frac{\sqrt{5}}{5}$•(-$\frac{2\sqrt{5}}{5}$)=$\frac{3}{5}$-$\frac{4}{5}$=-$\frac{1}{5}$.
点评 本题主要考查同角三角函数的基本关系,两角差的三角公式、二倍角公式的应用,属于基础题.

 教学练新同步练习系列答案
教学练新同步练习系列答案| A. | 若α∥β,m?α,n?β,则m∥n | |
| B. | 若m,n?α,m∥β,n∥β,则α∥β | |
| C. | m,n是异面直线,若m∥α,m∥β,n∥α,n∥β,则α∥β | |
| D. | 若α∥β,m∥α,则m∥β |
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{π}{4}$ | D. | 0 |
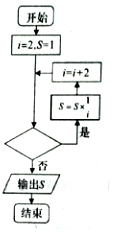 如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )| A. | i≤2019? | B. | i<2019? | C. | i≤2017? | D. | i≤2018? |
| A. | $-\frac{5}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{11}{8}$ |
 我国南宋时期的著名数学家秦九韶在他的著作《数学九章》中提出了秦九韶算法来计算多项式的值,在执行如图算法的程序框图时,若输入的n=5,x=2,则输出V的值为( )
我国南宋时期的著名数学家秦九韶在他的著作《数学九章》中提出了秦九韶算法来计算多项式的值,在执行如图算法的程序框图时,若输入的n=5,x=2,则输出V的值为( )