题目内容
已知函数f(x)=x2+2ax,x∈[-5,5].
(1)当a=-1时,求函数f(x)的最大值和最小值;
(2)求实数a的取值范围,使f(x)在区间[-5,5]上是减函数;
(3)求函数f(x)的最小值g(a),并求g(a)的最大值.
(1)当a=-1时,求函数f(x)的最大值和最小值;
(2)求实数a的取值范围,使f(x)在区间[-5,5]上是减函数;
(3)求函数f(x)的最小值g(a),并求g(a)的最大值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:1)当a=-1时,函数f(x)=(x-1)2-1,再利用二次函数的性质求得函数在[-5,5]上的最值.
(2)根据y=f(x)的对称轴为x=-a,且在区间[-5,5]上是单调减函数,可得-a≥5,由此求得a的范围.
(3)由于y=f(x)=(x+a)2+2-a2 的对称轴为x=-a,再根据对称轴和区间的关系分类讨论,根据函数的单调性求得g(a)的解析式,从而求得g(a)的最大值.
(2)根据y=f(x)的对称轴为x=-a,且在区间[-5,5]上是单调减函数,可得-a≥5,由此求得a的范围.
(3)由于y=f(x)=(x+a)2+2-a2 的对称轴为x=-a,再根据对称轴和区间的关系分类讨论,根据函数的单调性求得g(a)的解析式,从而求得g(a)的最大值.
解答:
解:(1)当a=-1时,函数f(x)=x2+2ax=x2 -2x=(x-1)2-1,
再由x∈[-5,5],可得当x=1时,函数取得最小值为-1,当x=-5时,函数取得最大值为35.
(2)∵y=f(x)=x2+2ax=(x+a)2-a2 的对称轴为x=-a,
且在区间[-5,5]上是单调减函数,可得-a≥5.
解得:a≤-5,故a的范围为:(-∞,-5].
(3)由于y=f(x)=x2+2ax=(x+a)2-a2 的对称轴为x=-a,
故当-5≤-a≤5时,即-5≤a≤5时,f(x)在区间[-5,5]上最小值g(a)=-a2.
当-a<-5时,即a>5时,由于f(x)在区间[-5,5]上单调递增,g(a)=f(-5)=25-10a,
当-a>5时,即a<-5时,由于f(x)在区间[-5,5]上单调递减,g(a)=f(5)=25+10a.
综上,g(a)=
.
当a<-5时,g(a)<-25; 当-5≤a≤5 时,-25≤g(a)≤0;当a>5时,g(a)<-25.
综合可得,g(a)的最大值为0,此时,a=0.
再由x∈[-5,5],可得当x=1时,函数取得最小值为-1,当x=-5时,函数取得最大值为35.
(2)∵y=f(x)=x2+2ax=(x+a)2-a2 的对称轴为x=-a,
且在区间[-5,5]上是单调减函数,可得-a≥5.
解得:a≤-5,故a的范围为:(-∞,-5].
(3)由于y=f(x)=x2+2ax=(x+a)2-a2 的对称轴为x=-a,
故当-5≤-a≤5时,即-5≤a≤5时,f(x)在区间[-5,5]上最小值g(a)=-a2.
当-a<-5时,即a>5时,由于f(x)在区间[-5,5]上单调递增,g(a)=f(-5)=25-10a,
当-a>5时,即a<-5时,由于f(x)在区间[-5,5]上单调递减,g(a)=f(5)=25+10a.
综上,g(a)=
|
当a<-5时,g(a)<-25; 当-5≤a≤5 时,-25≤g(a)≤0;当a>5时,g(a)<-25.
综合可得,g(a)的最大值为0,此时,a=0.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知m,n为不同的直线,α,β为不同的平面,则下列说法正确的是( )
| A、m?α,n∥m⇒n∥α |
| B、m?α,n⊥m⇒n⊥α |
| C、m?α,n?β,m∥n⇒α∥β |
| D、n?β,n⊥α⇒α⊥β |
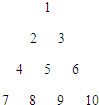 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为