题目内容

若
x2
a2
+
y2
b2
=1与x2+y2=（
b
2
+c）2总有四个交点，求离心率e的范围．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：
x2
a2
+
y2
b2
=1与x2+y2=（
b
2
+c）2总有四个交点，可得
b
2
+c＞b，进而可得4c2＞a2-c2，即可求离心率e的范围．
解答： 解：∵
x2
a2
+
y2
b2
=1与x2+y2=（
b
2
+c）2总有四个交点，
∴
b
2
+c＞b，
∴c＞
b
2
，
∴4c2＞a2-c2，
∴0＜e＜
5
5
．
点评：本题考查求离心率e的范围，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知二次函数f（x）=ax2+bx且f（2）=0，方程f（x）-1=0有两个相等的实数根．
（1）求函数f（x）的解析式；
（2）用定义证明f（x）在[1，+∞）上是减函数；
（3）当x∈[-
1
2
，
3
2
]时，利用图象求f（x）的最大值和最小值．
在△ABC中，a=1，b=2，cosC=
1
2
，则c=
 
．
△ABC的内角A，B，C的对边分别为a，b，c，b=5，c=7，a=3
2

（1）求cosA的大小
（2）△ABC面积的大小．
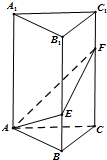如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，AA1=6，点E、F分别在棱BB1、CC1上，且BE=
1
3
BB1，C1F=
1
3
CC1．
（1）求异面直线AE与A1 F所成角的大小；
（2）求平面AEF与平面ABC所成角的余弦值．
已知函数f（x）=x2+2ax，x∈[-5，5]．
（1）当a=-1时，求函数f（x）的最大值和最小值；
（2）求实数a的取值范围，使f（x）在区间[-5，5]上是减函数；
（3）求函数f（x）的最小值g（a），并求g（a）的最大值．
设α、β为空间任意两个不重合的平面，则：
①必存在直线l与两平面α、β均平行；    
②必存在直线l与两平面α、β均垂直；
③必存在平面γ与两平面α、β均平行；    
④必存在平面γ与两平面α、β均垂直．
其中正确的是
 
．（填写正确命题序号）
已知f（x）=
x2+1，x∈[0，1]
x+1，x∈[-1，0)
，则下列四图中所作函数的图象错误的是（　　）
A、
B、
C、
D、
已知函数f（x）=
 
2x(x＜4)
 
f(x-1)(x≥4)
，则f（5）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网