题目内容
20.已知不等式9x2-logax<0,当$x∈({0\;,\;\;\frac{1}{3}})$时恒成立,则实数a的取值范围是[$\frac{1}{3}$,1).分析 不等式9x2-logax<0,当$x∈({0\;,\;\;\frac{1}{3}})$时恒成立?logax>9x2,当$x∈({0\;,\;\;\frac{1}{3}})$时恒成立,即[logax]min>[9x2]max,利用对数函数与二次函数的单调性可得loga$\frac{1}{3}$≥9×${(\frac{1}{3})}^{2}$,从而可得实数a的取值范围.
解答 解:不等式9x2-logax<0,当$x∈({0\;,\;\;\frac{1}{3}})$时恒成立?logax>9x2,当$x∈({0\;,\;\;\frac{1}{3}})$时恒成立,
∴[logax]min>[9x2]max,
又0<a<1,
∴y=logax在区间(0,$\frac{1}{3}$)上单调递减,又y=9x2在区间(0,$\frac{1}{3}$)上单调递增,
∴loga$\frac{1}{3}$≥9×${(\frac{1}{3})}^{2}$=1,
∴$\frac{1}{3}$≤a<1,
故答案为:[$\frac{1}{3}$,1).
点评 本题考查函数恒成立问题,依题意,得到当$x∈({0\;,\;\;\frac{1}{3}})$时,[logax]min>[9x2]max是关键,考查对数函数与二次函数的单调性的综合运用,漏掉等号是易错点,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.直线x-$\sqrt{3}$y+3=0的斜率是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
11.已知圆${x^2}+{y^2}+(4-2a)x-2\sqrt{3}ay+4{a^2}-4a-12=0$,定直线l经过点A(1,0),若对任意的实数a,定直线l被圆C截得的弦长始终为定值d,求得此定值d等于( )
| A. | $2\sqrt{7}$ | B. | $\sqrt{31}$ | C. | $\sqrt{34}$ | D. | $\sqrt{37}$ |
8.如图所示,程序据图(算法流程图)的输出结果为( )
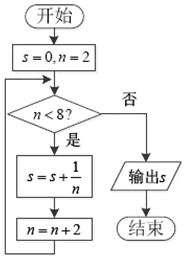

| A. | $\frac{3}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{11}{12}$ | D. | $\frac{25}{24}$ |
5.f(x)为奇函数,且x>0时,f(x)=x2-2x,则x<0时,f(x)=( )
| A. | f(x)=x2+2-x | B. | f(x)=x2-2-x | C. | f(x)=-x2+2-x | D. | f(x)=-x2-2-x |
9.在区间[-2,3]上随机取一个数x,则x∈[-1,1]的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
10.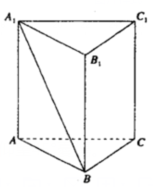 如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,侧棱AA1⊥面ABC,若AB=AA1,则直线A1B与AC所成角的余弦值为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,侧棱AA1⊥面ABC,若AB=AA1,则直线A1B与AC所成角的余弦值为( )
 如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,侧棱AA1⊥面ABC,若AB=AA1,则直线A1B与AC所成角的余弦值为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,侧棱AA1⊥面ABC,若AB=AA1,则直线A1B与AC所成角的余弦值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{14}}{2}$ | D. | $\frac{\sqrt{14}}{4}$ |