题目内容
直角三角形ABC中，CA=CB=
，M为AB的中点，将△ABC沿CM折叠，使A、B之间的距离为1，则三棱锥M-ABC外接球的体积为 ．
| 2 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离,球
分析：由已知中得三棱锥M-ABC的底面为边长为1的等边三角形，且MC与底面MAB垂直，故其外接球可转化为以MAB为底面，以MC为高的正三棱柱的外接球，求出球半径后，代入球体积公式，可得答案．
解答：
解：∵Rt△ABC中CA=CB=
，
∴AB=2，
又∵M为AB的中点，
∴MA=MB=MC=1，
故对折后三棱锥M-ABC的底面为边长为1的等边三角形，
如下图所示：
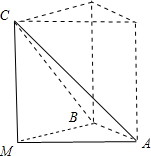
其外接球可化为以MAB为底面，以MC为高的正三棱柱的外接球，
设三棱锥M-ABC外接球的球心为O，
则球心到MAB的距离d=
MC=
，
平面MAB的外接圆半径r=
，
故三棱锥M-ABC外接球的半径R=
=
=
，
则外接球的体积为V=
πR3=
π(
)3=
故答案为：
．
| 2 |
∴AB=2，
又∵M为AB的中点，
∴MA=MB=MC=1，
故对折后三棱锥M-ABC的底面为边长为1的等边三角形，
如下图所示：
其外接球可化为以MAB为底面，以MC为高的正三棱柱的外接球，
设三棱锥M-ABC外接球的球心为O，
则球心到MAB的距离d=
| 1 |
| 2 |
| 1 |
| 2 |
平面MAB的外接圆半径r=
| ||
| 3 |
故三棱锥M-ABC外接球的半径R=
| d2+r2 |
|
|
则外接球的体积为V=
| 4 |
| 3 |
| 4 |
| 3 |
|
7
| ||
| 54 |
故答案为：
7
| ||
| 54 |
点评：本题考查的知识点是球的体积和表面积，其中根据已知条件求出球的半径是解答本题的关键．
练习册系列答案
相关题目
在平面直角坐标系n∈N+，n≥2）中，设A（-2，3），B（3，-2），沿x轴把直角坐标平面折成大小为
的二面角后，则线段AB的长度是（ ）
| 2π |
| 3 |
A、
| ||||||||
B、2
| ||||||||
C、3
| ||||||||
D、[
|
如图，在正三棱柱ABC-A1B1C1中，已知AA1=4，AB=2，E是BC的中点，D在棱AA1上．边长是2的正方体的外接球的表面积为（ ）
| A、12π | ||
B、4
| ||
| C、6π | ||
| D、4π |