题目内容
已知直线x=2π和y=4与坐标轴围成一个矩形,现向该矩形内随机投一点(该点落在矩形内任何一点是等可能的),则所投的点恰好在曲线y=
与x轴围成区域内的概率为( )
| 4-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:首先分别求出矩形和曲线y=
在第一象限部分的面积,然后利用几何概型的公式解答.
| 4-x2 |
解答:
解:由题意,矩形的面积为π×4=8π,曲线y=
在第一象限部分的面积为
π×22=π,
由几何概型的公式得所投的点恰好在曲线y=
与x轴围成区域内的概率为
=
;
故选A.
| 4-x2 |
| 1 |
| 4 |
由几何概型的公式得所投的点恰好在曲线y=
| 4-x2 |
| π |
| 8π |
| 1 |
| 8 |
故选A.
点评:本题是与面积有关的几何概率的计算,求解需要分别计算矩形的面积及阴影部分的面积,考查了利用积分计算不规则图象的面积.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
已知l,m,n是三条不同的直线,α,β,γ是三个不同的平面,下面命题正确的是( )
| A、若m⊥l,n⊥l,则m∥n |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若m∥l,n∥l,则m∥n |
| D、若m∥α,n∥α,则m∥n |
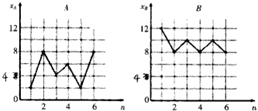 如图,样本A和B分别来自两个不同的总体,它们的样本平均数分别为
如图,样本A和B分别来自两个不同的总体,它们的样本平均数分别为. |
| xA |
. |
| xB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行如图的程序框图,算法执行完毕后,输出的S为( )


| A、8 | B、63 | C、92 | D、129 |
双曲线2x2-y2=8的实轴长是( )
A、2
| ||
| B、2 | ||
C、4
| ||
| D、4 |
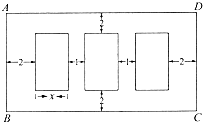 某公司因业务发展需要,准备印制如图所示的宣传彩页,宣传彩页有三幅大小相同的三个画面组成,每个画面的面积都是200cm2,这三个画面中都要绘制半径为5cm的圆形图案,为美观起见,每两个画面之间要留1cm的空白,三幅画周围要留2cm页边距,如图,设一边长x,所选用的彩页纸张面积为S
某公司因业务发展需要,准备印制如图所示的宣传彩页,宣传彩页有三幅大小相同的三个画面组成,每个画面的面积都是200cm2,这三个画面中都要绘制半径为5cm的圆形图案,为美观起见,每两个画面之间要留1cm的空白,三幅画周围要留2cm页边距,如图,设一边长x,所选用的彩页纸张面积为S