题目内容
13．已知$A（\sqrt{3}，2），F（\sqrt{3}，0）$，P是椭圆$\frac{x^2}{4}+{y^2}=1$上的任一点，则|PA|-|PF|的取值范围是[0，2]．分析 利用椭圆的定义以及三角形的性质推出结果即可．
解答 解：|PA|-|PF|=（|PA|+|PF1|）-2a≥|AF1|-4=0，
P为线段AF1与椭圆的交点时取“=”．|PA|-|PF|≤|AF|=2，P为AF延长线与椭圆的交点时取“=”．
故答案为：[0，2]．
点评 本题考查椭圆的简单性质的应用，考查计算能力．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
1．直线y=mx+1与曲线x=2+$\sqrt{1-{y}^{2}}$的图象始终有交点，则m的取值范围是（ ）
| A． | （-1，0） | B． | [-1，0] | C． | （-1，-$\frac{1}{3}$） | D． | [-1，-$\frac{1}{3}$] |
8．若命题“p且q”为假，且p为真，则（ ）
| A． | “p或q”为假 | B． | q为假 | C． | q为真 | D． | 不能判断q的真假 |
5．已知N是自然数集，在数轴上表示出集合A，如果所示，则A∩N=（ ）
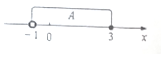
| A． | {-1，0，1，2，3} | B． | {0，1，2，3} | C． | {1，2，3} | D． | {2，3} |