题目内容
3．计算：（$\frac{1}{3}$）-1+|1-$\sqrt{3}$|-2sin60°+（π-2016）0-$\root{3}{8}$．分析 根据指数幂的运算性质计算即可．
解答 解：原式=$3+\sqrt{3}-1-2×\frac{{\sqrt{3}}}{2}+1-2$=1．
点评 本题考查了指数幂的运算性质，属于基础题．
练习册系列答案
相关题目
8．高斯函数f（x）=[x]的函数值表示不超过x的最大整数，如[-2.3]=-3，[1.2]=1．设函数g（x）=x-f（x），函数u（x）={sinπx}，则下列说法正确的是（ ）
| A． | 函数g（x）与u（x）的值域相同 | B． | 函数g（x）与u（x）的最小正周期相同 | ||
| C． | 函数g（x）与u（x）的单调区间相同 | D． | 函数g（x）与u（x）奇偶性相同 |
11．设F1（-c，0），F2（c，0）是椭圆C1：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）与双曲线C2有公共焦点F1、F2，（F1、F2分别为左、右焦点），它们在第一象限交于点M，离心率分别为e1和e2，线段MF1的垂直平分线过F2，则$\frac{{{e_2}-{e_1}}}{{{e_1}{e_2}}}$的值为（ ）
| A． | $2\sqrt{2}$ | B． | $3\sqrt{2}$ | C． | 3 | D． | 2 |
18．
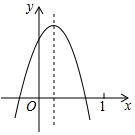已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①b＜0，c＞0；②a+b+c＜0；③方程的两根之和大于0；④a-b+c＜0，其中正确的个数是（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①b＜0，c＞0；②a+b+c＜0；③方程的两根之和大于0；④a-b+c＜0，其中正确的个数是（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
8．已知函数f（x）=$\left\{\begin{array}{l}{2^x}，x≤1\\ ln（{x-1}），1＜x＜2\end{array}$，若存在实数a，当x＜2时，f（x）≤ax+b恒成立，则实数b的取值范围是（ ）
| A． | [1，+∞） | B． | [2，+∞） | C． | [3，+∞） | D． | [4，+∞） |
15．已知点（a，b）在圆C：x2+y2=r2（r≠0）的外部，则ax+by=r2与圆C的位置关系是（ ）
| A． | 相切 | B． | 相离 | C． | 内含 | D． | 相交 |
12．函数f（x）=（kx+4）lnx-x（x＞1），若f（x）＞0的解集为（s，t），且（s，t）中只有一个整数，则实数k的取值范围为（ ）
| A． | （$\frac{1}{ln2}$-2，$\frac{1}{ln3}$-$\frac{4}{3}$） | B． | （$\frac{1}{ln2}$-2，$\frac{1}{ln3}$-$\frac{4}{3}$] | C． | （$\frac{1}{ln3}$-$\frac{4}{3}$，$\frac{1}{2ln2}$-1] | D． | （$\frac{1}{ln3}$-$\frac{4}{3}$，$\frac{1}{2ln2}$-1） |