题目内容
数列{an}是公比为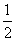 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=nλ·bn+1(λ为常数,且λ≠1).
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=nλ·bn+1(λ为常数,且λ≠1).
(1)求数列{an}的通项公式及λ的值;
(2)比较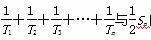 的大小.
的大小.
解析:(1)由题意得(1-a2)2=a1(a3+1),
即
解得a1=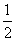 ,∴ an=
,∴ an= n.
n.
又
解得 或
或 (舍),∴ λ=
(舍),∴ λ=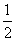 .
.
(2)由(1)知Sn=1- n,
n,
∴ 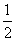 Sn=
Sn=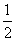 -
- n+1≥
n+1≥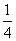 ,①
,①
又Tn=4n2+4n,∴  =
=
∴
=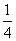

=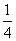
 <
<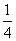 ,②
,②
由①②,得

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 现输入s和货物的吨数ω,画出计算总运费的流程图.
现输入s和货物的吨数ω,画出计算总运费的流程图. D.
D. 


 时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f
时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f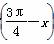 是( )
是( )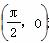 对称
对称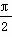 对称
对称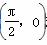 对称
对称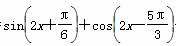 +sin 2x,x∈[0,π].
+sin 2x,x∈[0,π].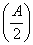 =
=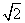 ,a=2,b=
,a=2,b=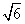 ,求角C.
,求角C.