题目内容
设两个向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
解: ∵ e1·e2=|e1|·|e2|·cos60°=2×1× =1,(2分)
=1,(2分)
∴ (2te1+7e2)·(e1+te2)
=2te +7te
+7te +(2t2+7)e1·e2
+(2t2+7)e1·e2
=8t+7t+2t2+7=2t2+15t+7.(4分)
因为向量2te1+7e2与向量e1+te2的夹角为钝角,所以(2te1+7e2)·(e1+te2)<0,
即2t2+15t+7<0,解得-7<t<- .(9分)
.(9分)
当向量2te1+7e2与向量e1+te2反向时,
设2te1+7e2=λ(e1+te2),λ<0,
则 2t2=7t=-
2t2=7t=- 或t=
或t= (舍).(12分)
(舍).(12分)
故t的取值范围为

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 +(m2+2m-3)i,当m为何值时.
+(m2+2m-3)i,当m为何值时. ,则顶点D的坐标为________.
,则顶点D的坐标为________. B.4
B.4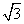

 =( )
=( ) a+b D.a+
a+b D.a+